LIGHT – PHYSICS NOTES FORM THREE
Reflection of Light from Curved Mirrors
Difference between Concave and Convex Mirrors
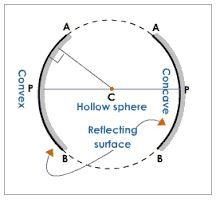
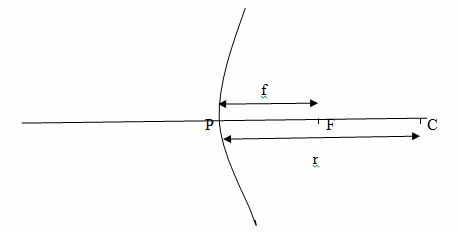
Explain the terms principle, axis, pole, principle focus and radius of curvature as applied to curved mirrors
Terms used in studying curved mirrors
- Centre of curvature (C):the centre of the sphere of which a mirror is a part of.
- Radius of curvature (r): the radius of sphere of which a mirror is a part of. Radius of curvature is double the focal length. That is r=f/2.
- Pole (P): the central point of the reflecting surface of spherical mirror (curved or convex mirror).
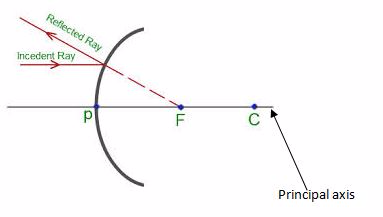
- Principal axis:the straight line joining the centre of curvature (C) and the pole (P).
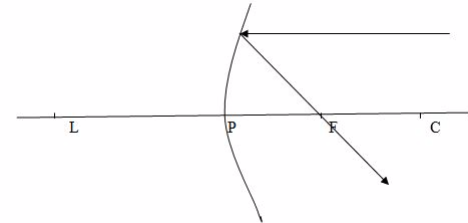
- Principal focus (F):the point on the principal axis where light rays tend to intersect after being reflected. This point is between centre of curvature and the pole. In concave mirror, parallel rays to the principal axis meet at the principal focus after reflection. In convex mirror, parallel rays to the principal axis appear to originate from the principal focus behind the mirror after reflection.
- Focal length (f): the distance from the pole of the mirror to the principal focus. Focal length is half the radius of curvature.
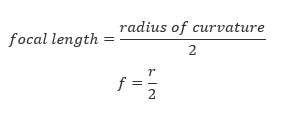
The Images Formed by a Curved Mirror
Locate the images formed by a curved mirror
Case 1
Case 2
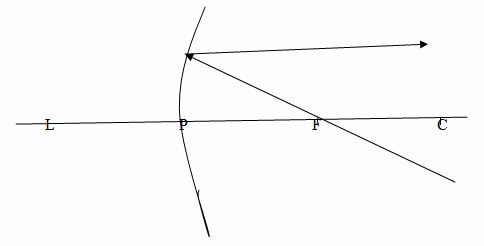
Case 3
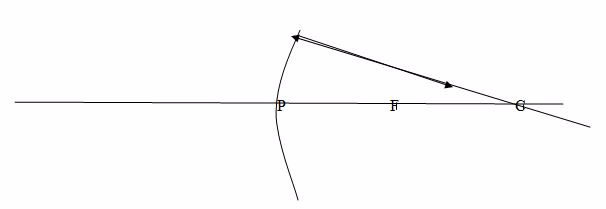
- The image is between C and F
- The image is smaller than the object
- The image is inverted (upside down)
- The image is real
- The image is formed at C
- The image has the same size as object
- The image is inverted (upside down)
- The image is real.
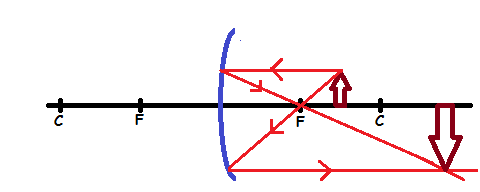
- The image is real
- The image is large than object
- The image is formed beyond C
- The image is inverted (upside down)

- The image is formed at infinity (x)
- The image is formed beyond C
- The image is large than object
- The image is Real
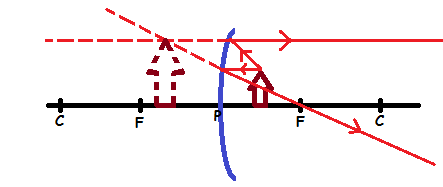
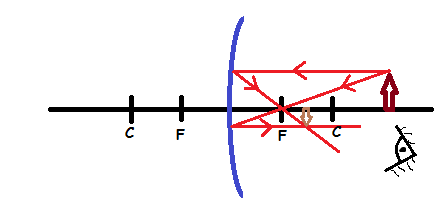
- The image is virtual
- The images is upright
- The image is formed behind the mirror
- The image is large than the object
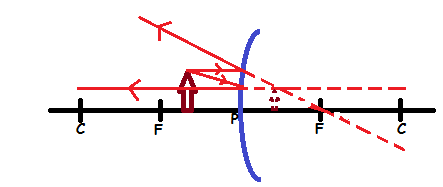
- The image is virtual
- The image is upright
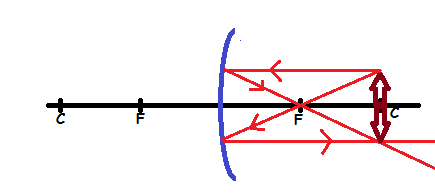
- The image is smaller than object (diminished)
- The image is formed behind the mirror.
The Mirror formula

- Real images are given a positive ‘+’ sign.
- Virtual images are given a negative ‘-‘ sign.
- Distances of real objects and images are given positive ‘+’sign.
- Distances of virtual images are given negative ‘-‘ sign.
- A real focal length is given a positive ‘+’ sign.
- A virtual focal length is given a negative ‘-‘ sign.
Magnification

- Height of object, Ho = 2cm
- Object distance, U= 8cm
- Radius of curvature, r = 10cm
- Focal length,f =8cm
- Choose suitable scale.
- Say 1cm represents 5cm
- Height of object, Ho = 2cm
- Object distance, U= 2cm
- Focal length, F = 2.5cm
The Focal Length of a Concave Mirror
Convex and Concave Mirrors in Daily Life
- Driving mirrors
- Shaving mirrors
- Reflectors
Question Time 1
Question Time 2
Refraction of Light
The Concept of Refraction of Light
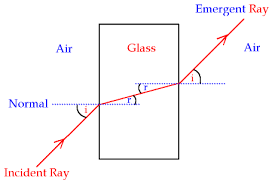
The Laws of Refraction
First law of refraction
Second law of refraction
The Refraction Index of a Material
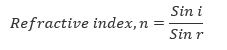
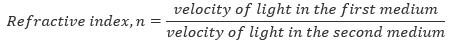
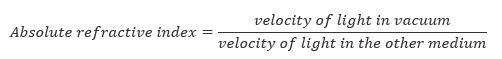
The refractive indices between air and some common media is given below:
| Medium | Refractive index (n) |
| Diamond | 2.417 |
| Ethanol | 1.360 |
| Glass (Crown) | 1.520 |
| Quartz | 1.553 |
| Water (at 20ºC0 | 1.333 |
| Air (at stp) | 1.00029 |
Real and Apparent Depth
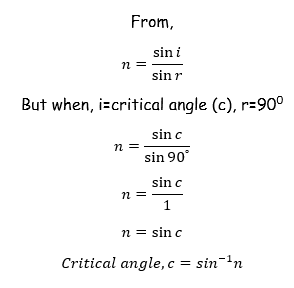
- Light must be travelling from a more dense to less dense medium.
- Light must incident at the boundary at an angle greater than the critical angle (C).
- Used in telecommunications to carry telephone calls over vast distance, without loss of intensity and without interference.
- Used in endoscope to view inside a patient body for example inside stomach. Light is carried into the stomach through a bunch of fibres and is reflected into small camera, which then displays a picture on a screen.
Refraction of Light by Rectangular Prism

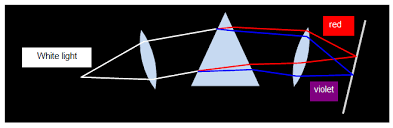
Activity 1
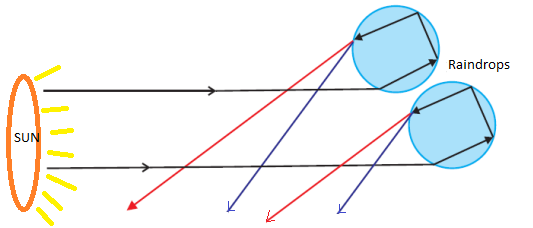
- Primary rainbow
- Secondary rainbow
Primary rainbow
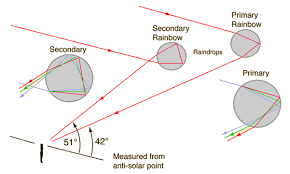
Secondary rainbow
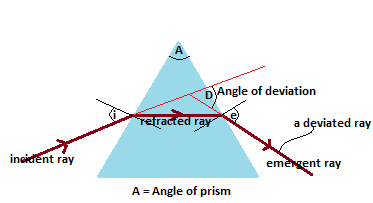
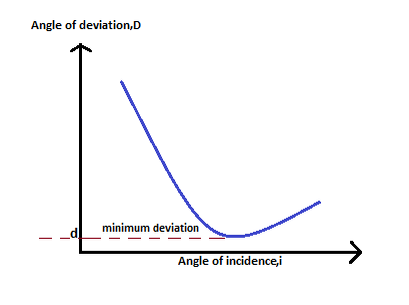
The Angles of Deviation and Minimum Deviation

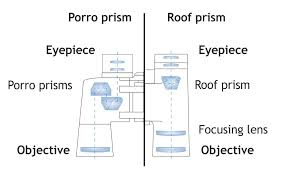
A Simple Prism Binocular
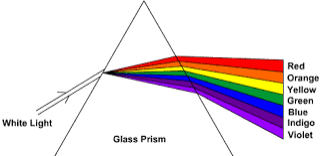
Colours of Light
The Component of White Light
- Primary colour of light
- Secondary colour of light
Primary colour of light
- Red
- Green
- Blue
Secondary colours of light
| Primary color | Secondary color | |
| Red + Blue | Magenta | |
| Red + Green | Yellow | |
| Blue + Green | Cyan |
Colours of White Light
- Red + Blue+ Green – White light
- Red + Cyan – White light
- Blue + Yellow – White light
- Green + Magenta – White light
The Appearances of Coloured Object under White Light
- Primary coloured pigment (paints)
- Secondary coloured pigment (paints)
Primary, Secondary and Complementary Colours of Light
Secondary colour pigments
Difference between Additive and Subtractive Combination of Colours
Colour Mixing by Substration
- Magenta + Cyan
- Magenta = ( Blue) + ( Red)
- Cyan = (Blue) + (green)
- Magenta + yellow
- Magenta = (Blue) + (Red)
- Yellow = (Green) + (Red)
- Cyan + yellow
- Cyan = (Blue) + (Green)
- Yellow = (Red) + (Green)
Refraction of Light by Lenses
- Convex lens -they are thicker at the middle than at the edges.
- Concave lens– they are thinner at the middle than at the edges.

The Focal Length of a Lens
Determine practically the focal length of a lens
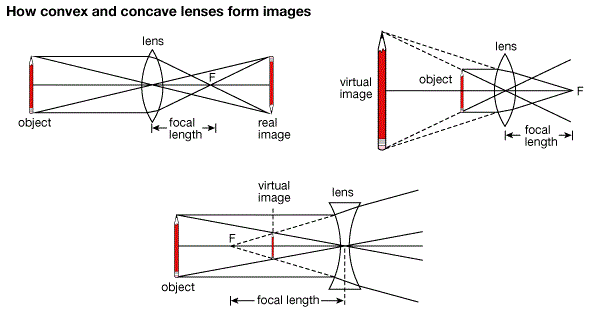
The Immage Formed by a Lens
Locate the image formed by a lens
- A ray parallel to the principal axis passes through or appears to diverge from the principal focus after refraction.
- A ray of light passing through the principal focus of a lens is refracted parallel to the principal axis of the lens.
- A ray of light through the optical center of the lens continues throughundeviated(Not change direction)
The position, Size and Nature of the Image formed by Lens
Activity 2
- Take a convex lens. Find its approximate focal length in a way described in Activity 11.
- Draw five parallel straight lines, using chalk, on a long Table such that the distance between the successive lines is equal to the focal length of the lens.
- Place the lens on a lens stand. Place it on the central line such that the optical centre of the lens lies just over the line.
- The two lines on either side of the lens correspond to F and 2F of the lens respectively. Mark them with appropriate letters such as 2F1, F1, F2and 2F2, respectively.
- Place a burning candle, far beyond 2F1to the left. Obtain a clear sharp image on a screen on the opposite side of the lens.
- Note down the nature, position and relative size of the image.
- Repeat this Activity by placing object just behind 2F1, between F1and 2F1at F1, between F1and O. Note down and tabulate your observations.
The nature, position and relative size of the image formed by convex lens for various positions of the object is summarized in the table below:
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At focus F2 | Highly diminished, point-sized | Real and inverted |
| Beyond 2F1 | Between F2and 2F2 | Diminished | Real and inverted |
| At 2F1 | At 2F2 | Same size | Real and inverted |
| Between F1and 2F1 | Beyond 2F2 | Enlarged | Real and inverted |
| At focus F1 | At infinity | Infinitely large or highly enlarged | Real and inverted |
| Between focus F1and optical centre O | On the same side of the lens as the object | Enlarged | Virtual and erect |
Activity 3
- Take a concave lens. Place it on a lens stand.
- Place a burning candle on one side of the lens.
- Look through the lens from the other side and observe the image. Try to get the image on a screen, if possible. If not, observe the image directly through the lens.
- Note down the nature, relative size and approximate position of the image.
- Move the candle away from the lens. Note the change in the size of the image. What happens to the size of the image when the candle is placed too far away from the lens.
Nature, position and relative size of the image formed by a concave lens for various positions of the object
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At focus F1 | Highly diminished, point-sized | Virtual and erect |
| Between infinity and optical centre O of the lens | Between focus F1and optical centre O | Diminished | Virtual and erect |






































Leave a Reply