TOPIC 1: APPLICATIONS OF VECTORS-PHYSICS NOTES FORM THREE
Difference between Scalar and Vector Quantities
Scalar Quantities
These are physical quantities which have magnitude only. Examples of scalar quantities include mass, length, time, area, volume, density, distance, speed, electric current and specific heat capacity.
Vector Quantities
Vectors Representation
A vector quantity can be represented on paper by a direct line segment.

- The length of the line segment represents the magnitude of a vector.
- The arrow head at the end represents the direction.
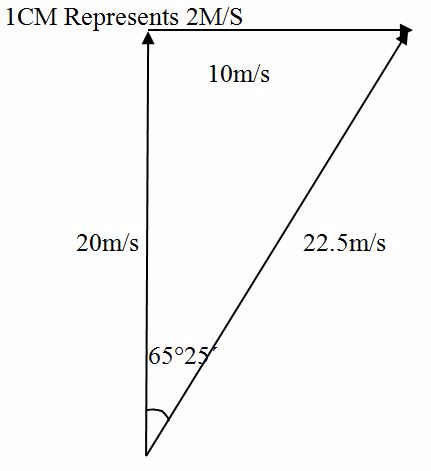
- Triangle method
- Parallelogram method.
Triangle Method
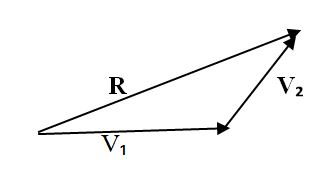
- V1 – First vector
- V2 – Second vector
- R – Resultant vector
Solution
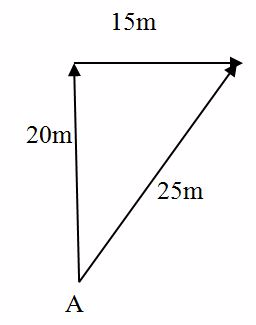
- Tan Q = (Opposite /Adjacent)
- Tan Q = 3cm /4cm
- Q = Tan -1 (3/4)
- Q = Tan -1(0.75)
- Q = 35º51”
The Resultant displacement is 25m ad direction Q = 36º51”
The Triangle and Parallelogram Laws of Forces
State the triangle and parallelogram laws of forces
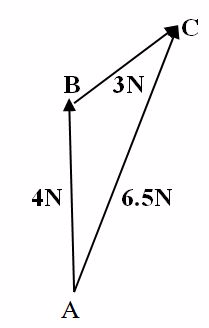
Triangle Law of Forces
Triangle Law of Forces states that “If three forces are in equilibrium and two of the forces are represented in magnitude and direction by two sides of a triangle, then the third side of the triangle represents the third force called resultant force.”
Parallelogram Method
The Parallelogram Law states that “If two vectors are represented by the two sides given and the inclined angle between them, then the resultant of the two vectors will be represented by the diagonal from their common point of parallelogram formed by the two vectors”.
Example 4
Solution
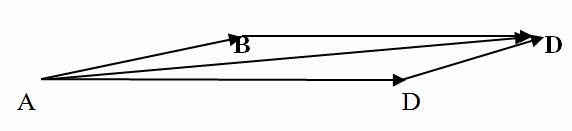
The lineAC of the parallelogram ABCD represents the resultant force of AB and AD in magnitude and direction.
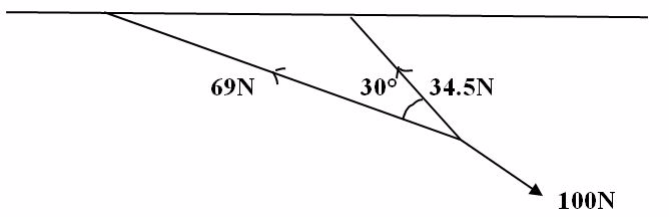
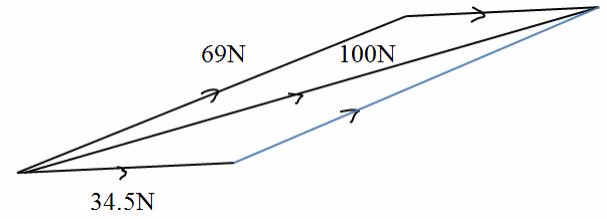
Note: Equilibrant forces are those that act on a body at rest and counteract the force pushing or pulling the body in the opposite direction.






















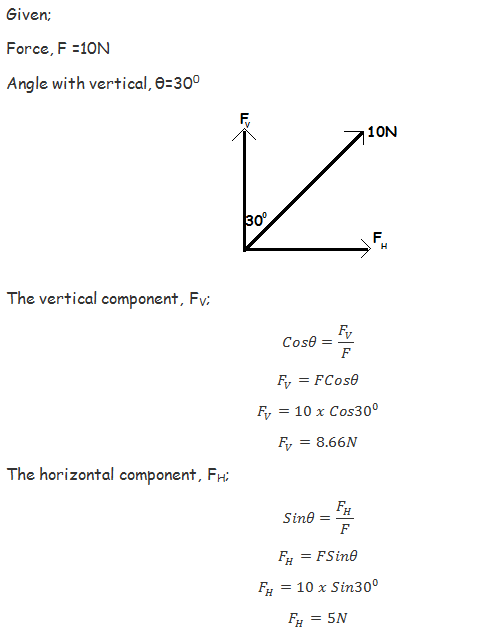









Leave a Reply