Density and Relative Density
Density is an important concept for scientists and engineers because it is useful in determining the characteristics of a material.
Engineers must think of the density of the materials before marine and air transport vessels can be designed and built so that they will float.
For example, aluminium alloy as one of the materials used in aircraft construction substituted steel because aluminium is less dense than steel.
In this lesson, you will learn the concept of density, how to determine the densities of solids and liquids, the concept of relative density and the determination of the relative density of solids and liquids.
The competencies developed are useful in designing and constructing of models for marine and air transport vessels so that they will float.
Moreover, you will acquire skills in identifying the purity of a substance and estimating the composition of different types of mixtures.
Concept of density
Suppose you measure the mass of three blocks made up of glass, iron, and wood whose size are identical shown in Figure below.
You will find that the masses of all blocks are different although their volumes are similar.



The iron block will have a greater mass than the glass block which has a greater mass than the wooden block. The difference in mass arises from the way the particles of the blocks are packed together.
This suggests that a comparison of the mass of a substance and its volume leads to an important physical quantity called density. This quantity is the measure of how the constituent particles of a substance are parked in a unit volume.
If particles are closely packed in a small volume of a substance, the substance is said to have high density and vice versa. Figure below shows high and low density substances.

Thus, density is the extent to which the particles of a substance are closely packed in a particular substance. The more compact the particles are in a particular substance, the higher the density of that substance.

The relationship between the density, mass, and volume of a substance can easily be remembered by the density-mass-volume triangle, shown in Figure below

From the triangle, the horizontal line that separates mass (m) and the other variables represents division sign.
So, whenever it is required to find density (ρ) or volume (V), mass (m) is divide by either volume (V) or density (ρ), respectively.
That is,
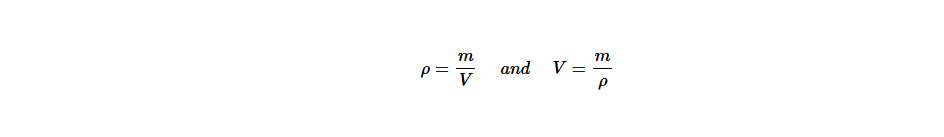
On the other hand, the vertical line that separates ρ and V represents the multiplication. Therefore, whenever it is required to find m, ρ and V are multiplied. Thus, m = ρ ×V.
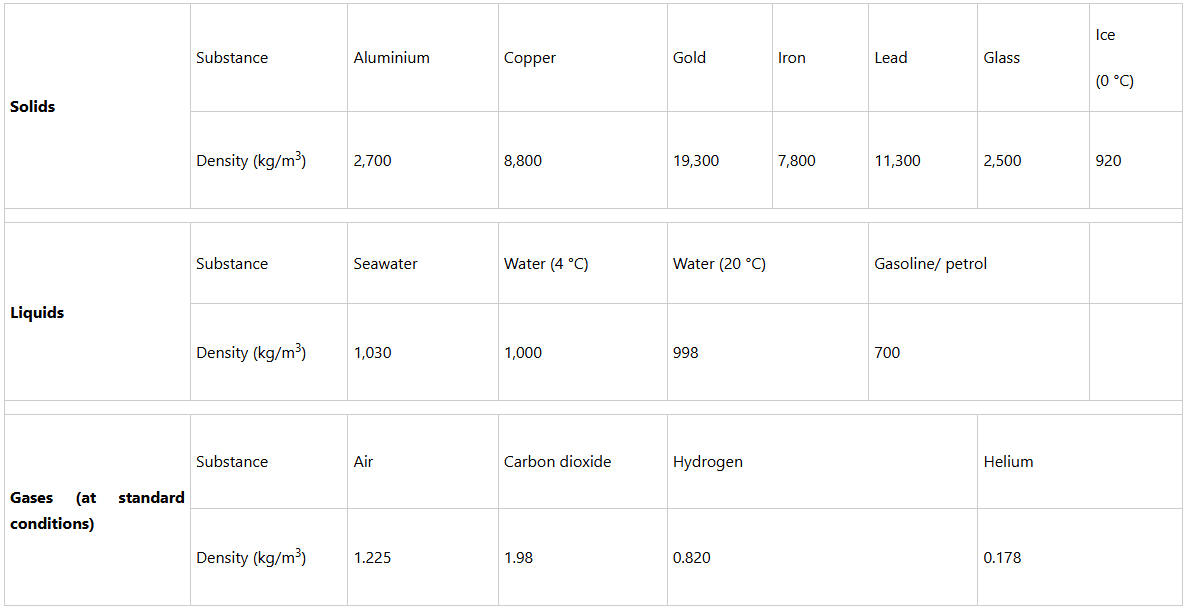
Density is an intrinsic property of matter since it is independent of the number of particles contained in the materials. The densities of common substances are given in Table
Activity 1
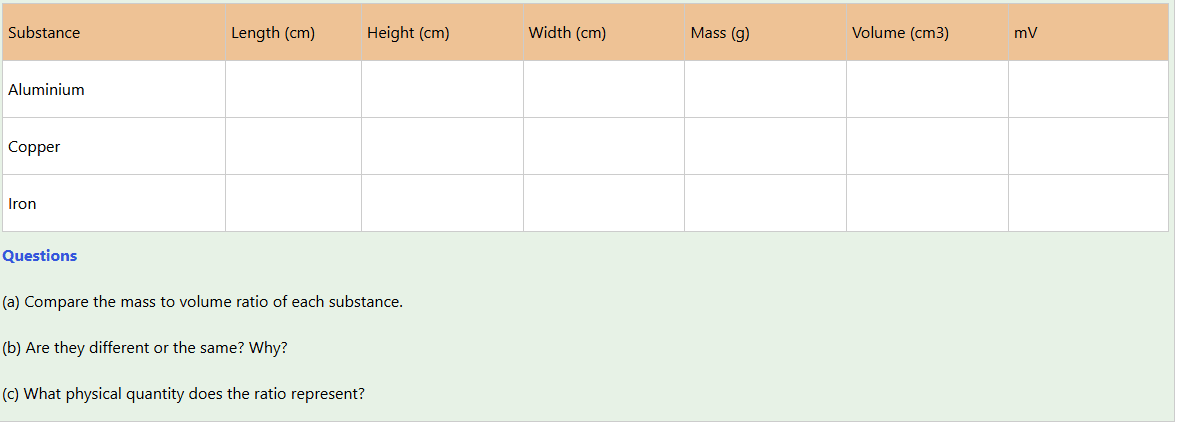
Aim: To determine the mass to volume ratio for given objects.
Materials: Vernier calliper, beam balance, three identical blocks of different materials as shown in Figure 4.4 (for instance, aluminium, copper, and iron, respectively)
Procedure
1. Measure the length, height and width of each object.
2. Measure the mass of each block.
3. Record all observations using the following table.

Example 1
What would be the density of a glass block calculated based on its dimensions of 0.12 m × 0.04 m × 0.10 m and a mass of 1.2 kg?




Determination of density of a substance
A technique used in the determination of density of a substance depends on the properties of the substance. For a given substance, the appropriate method for measuring its mass and volume must be used. Once the measured values of mass and volume are known, the density of a substance can be calculated.It is important to note that different techniques are used to determine the density of solids, liquids and gases.
Determination of density of solid
The density of a solid object can be determined using techniques that depend on the shape of the object under observation. The shape of the object may be regular or irregular. For the case of a regular shape, one needs to measure its mass and dimensions. The density is then calculated using the formula ρ=m/V
, where volume is calculated using the dimensions of the objects. If the shape of the object is irregular, its volume can be measured using the measuring cylinder or eureka can as discussed in Chapter Two of this book.
Activity 2
Aim: To determine the density of regular shaped objects.
Materials: Wood blocks, glass block, textbooks, ruler and test tube
Procedure
1. Measure and record the length, height and width of each object.
2. Measure and record the mass of each object.
3. Calculate the volume of each object using a proper formula.
4. For each object calculate its density.
5. Report your results in a tabular form.
Question
Compare the densities of different objects.

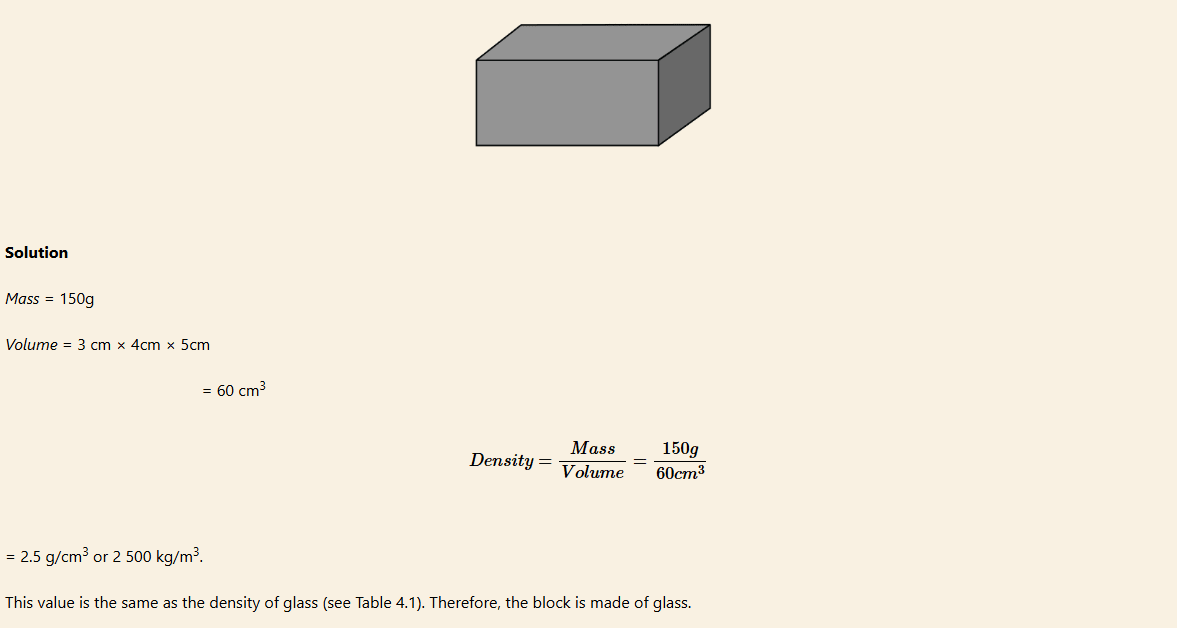
Example 3
In a physics exercise, a student was given a rectangular shaped block to find its density and predict using a standard density table the type of material composing the block.
The student measures the mass and dimensions of the block and obtained 150 g and 3 cm × 4 cm × 5 cm, respectively. What possible conclusion did the student make?
Task 1
Suppose, you have a wooden block, metre ruler, and a beam balance and you want to determine the density of the wooden block:
(a) What information do you need in order to calculate the density of the wooden block?
(b) How would you obtain such information using the available resources?
Activity 3
Aim: To determine the density of an irregular shaped object.
Materials: Eureka can, beaker, measuring cylinder, string, triple beam balance, or digital beam balance and stones of different shapes
Procedure
1. Measure the mass of irregular stones using a beam balance and record your results in Table
2. Measure the volume of each stone and record in Table

3. determine the density of each stone.
4. compare the densities of different stones.
Question
What can you conclude from your observation?

Example 4
An irregular solid X has a mass of 50 g. When it is totally immersed in the water of volume 60 cm3, the final water volume is 70 cm3. Calculate the density of the irregular solid X.


Task 2
If you want to determine the density of stone:
(a) Suggest the suitable instruments/ apparatus you may need to carry out this task.
(b) If some of the apparatus are not there in your home environment, what alternative you may use to carry out the activity?
Density of insoluble granules
Determination of the density of small insoluble particles such as sand grains is also possible. Unlike other solids, granules must be held in some type of container while being measured. This could be realised by using a density bottle.
A density bottle has a precisely measured volume, usually 25 ml, 50 ml, or 100 ml and a tight-fitting stopper with a small hole to allow excess liquid to escape. It is mostly used in studying and analysing the relative densities of two immiscible liquids. Figure 4.5 shows parts of a density bottle.

The following steps are to be followed when using a density bottle to measure the density of insoluble granules such as sand.
1. Measure the mass of the empty density bottle with its stopper; record as m0 .
2. Remove the stopper, add a small amount of sand to the bottle and replace the stopper. Measure the mass of the bottle containing sand and its stopper; record this mass as m1.
3. The difference between m1 and m0 gives the mass of the sand. Mass of sand = (m1 − m0) .
4. Remove the stopper, add water into the bottle until the bottle is full, replace the stopper.
5. Measure the mass of the bottle containing water and sand as m2.
6. The difference between m2 and m1 gives the mass of the water added to the bottle. Mass of water is (m2 − m1).
7. Since the density of water is 1 g/cm3, the volume added to the bottle is given in cm3, which is numerically equal to the mass of the water in grammes.
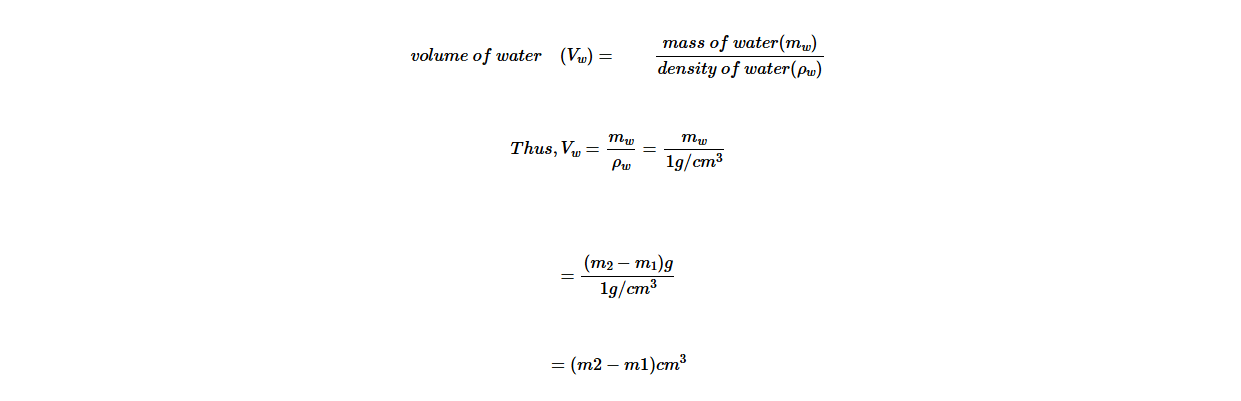

Activity 4
Aim: To determine the density of lead shots.
Materials: Density bottle, lead shots and water

Procedure
1. Find the mass m0 of density bottle when empty.
2. Put some lead shots in the bottle, then find the mass, m1 of a bottle and lead shot.
3. Pour water into the bottle until it is full. Find the mass, m2 of a bottle, lead shot and water.
4. Finally, find the mass, m3 when the bottle is filled with water only, Figure 4.6 illustrates the procedure.


Density of a liquid
The density of a liquid can also be calculated if its mass and volume are known. Thus, the density of a liquid can be determined through the following steps:
1. Measure an empty beaker; record it as m0.
2. Using a burette, run out a known volume (V) of the liquid into the beaker and measure the mass; record it as m1 .
3. Subtract m0 from m1 to get the mass of the liquid, that is,mass of liquid = (m1 − m0 ) .
4. Calculate the density of the liquid by dividing mass obtained in step (3) by the known volume of liquid, that is;
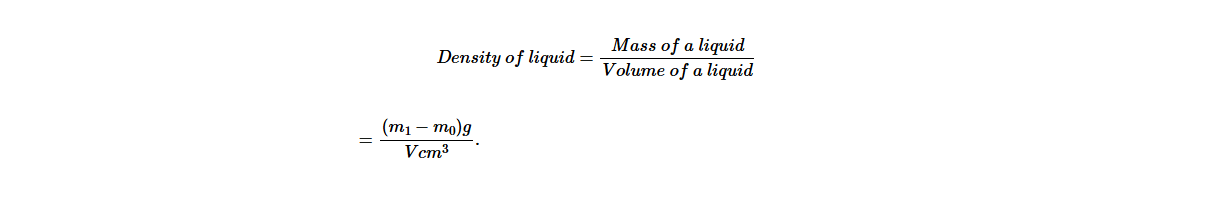
Example 5
In an experiment to determine the density of liquid Y, a Form One student obtained the following results: Mass of beaker = 500 g and Mass of beaker + liquid (25 cm3) = 600 g. What did the student obtain as the density of liquid Y?


Activity 5
Aim: To determine the densities of kerosene and milk.
Materials: Beakers, pipettes, beam balance, kerosene and milk
Procedure
1.Weigh a dry empty beaker using a weighing balance and record it as, m0.
2. Use a pipette to accurately measure 20 ml of kerosene and transfer it into the weighed beaker.
3. Measure the mass of the beaker with kerosene and record it as m1.
4. Repeat steps 1 to 3 for milk.
Questions
(a) Calculate the mass of the 20 ml of kerosene and milk.
(b) Calculate the density of kerosene and milk.
(c) Why is it necessary to measure the mass of the empty beaker?


Relative Density of a Substance
It is common practice to express the density of a substance such as solid, liquid and gas (air) in relation to the density of water. The ratio between density of substance to the density of water is called relative density, R.D. Mathematically, it can be expressed as;
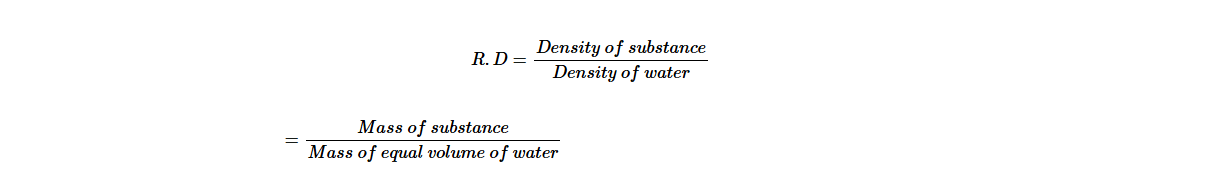
The relative density has no unit, since it is expressed as the ratio of the same quantity.
Relative density is also known as the specific gravity (S.G). It indicates how many times a substance is denser compared to water. A substance is denser than water if its relative density is larger than 1 and the substance is less dense than water if its relative density is less than 1.
EXAMPLE 6

EXAMPLE 7

Relative density of a solid
Activity 6
Aim: To find the relative density of a solid material.
Materials: Eureka can, measuring cylinder, stone, beam balance, water, string, beaker


Procedure
1. Find the mass, m0 of the solid by using a beam balance.
2. Place an empty dry beaker of mass m1 under the spout of the eureka can, as shown in Figure 4.7 (a).
3. Fill the eureka can with water until it just begins to overflow, as shown in Figure 4.7 (a).
4. Lower gently the solid into the water with the help of a thin string until it is completely immersed, as shown in Figure 4.7 (b).
5. Let the water overflow into the beaker under the spout. Measure the mass of beaker containing the overflow water. Call this m2 .
Results
Mass of a solid = m0
Mass of dry empty beaker = m1
Mass of beaker and water = m2
Mass of equal volume of water = (m2 – m1)
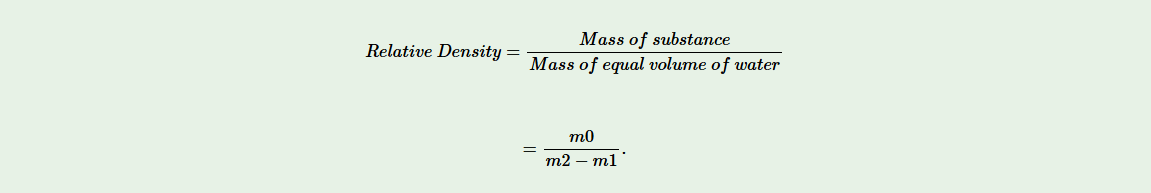

Example 8
A block of metal has a mass of 264 g. The block is totally immersed in water filling up a eureka can. If 24 g of water overflows through the spout of the can into a beaker, calculate the relative density of the metal.


Determination of relative density of a liquid
The relative density of a liquid can be determined using a relative density bottle shown in Figure 4.8. A bottle is fitted with a stopper made of ground glass having a narrow hole. The hole enables air to escape from the bottle when it is being filled with a liquid.

Relative density of a liquid can be determined using the following procedure:
1. Find the mass of an empty bottle, m0 .
2. Fill in the bottle with the liquid and measure the mass of the bottle with its contents. Record this mass as m1.
3. Empty the bottle, clean and dry it thoroughly.
4. Fill in the bottle with water and measure the mass of the bottle containing water. Record this mass m2.
Hence, mass of liquid = (m1 − m0)
Mass of an equal volume of water = (m2 − m0).
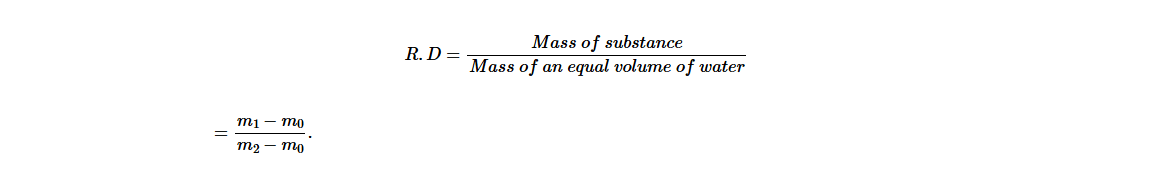
Activity 7
Aim: To determine the relative density of cooking oil.
Materials: Relative density bottle, cooking oil, beam balance and water

Procedure
1. Measure the mass of an empty relative density bottle with its stopper. Record the mass as m0.
2. Fill in the bottle with cooking oil, replace the stopper and wipe out any excess liquid. Measure the mass. Record the mass as m1.
3. Replace the cooking oil with water and measure the mass. Record it as m2 .
Questions
(a) Calculate the relative density of cooking oil.
(b) What is the significance of a narrow hole in the relative density bottle?

The relative density of cooking oil can be obtained by:
(i) Finding the mass of cooking oil, (m1 − m0) .
(ii) Finding the mass of an equal volume of water, (m2 − m0).
(iii) Calculating the relative density of cooking oil,

(iv) The narrow hole in the stopper enables air to escape from the bottle when it is being filled with a liquid.
Example 9
In an experiment to determine the relative density of liquid X, Form One physics students obtained the following results after various measurements.
Mass of an empty relative
density bottle = 15 g
Mass of bottle + liquid X = 35 g
Mass of bottle + water = 40 g
Volume of bottle = 25 cm3
Calculate,
(a) The density of water in kg/m3.
(b) The density of liquid X in kg/m3.
(c) The relative density of liquid X.
Solution

Exercise 1
Answer all questions
1. (a) What is the volume of 2400 kg of gasoline (petrol) if its density is 0.7 g/cm3?
(b) Use the table below to answer the questions that follow.
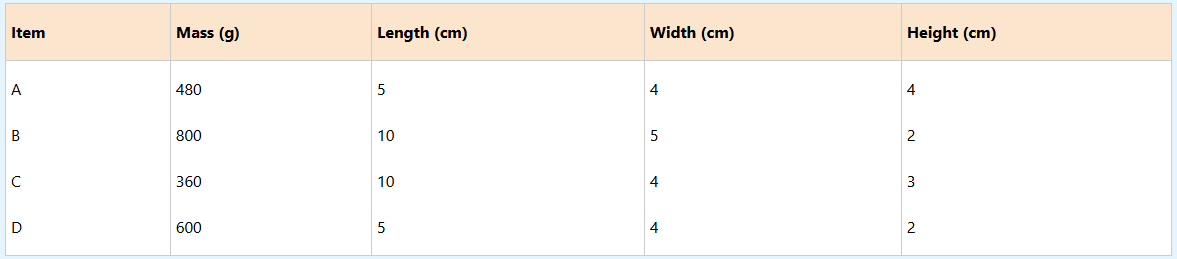
(i) Which item is dense?
(ii) Which item is the least dense?
2. The water collected in a measuring cylinder during an experiment using a eureka can is 30 cm3. When the object that displaced this volume was dried and weighed, its mass was found to be 90 g. Calculate its density.
3. A Form One student in Physics class obtained the following results from an experiment:
Mass of an empty beaker = 48 g
Mass of beaker + liquid M = 60 g
If she had used a 25 cm3 pipette to transfer liquid M to the beaker, calculate the density of the liquid M.
4. What is relative density? Express relative density in terms of mass.
Applications of the concept of density and relative density in everyday life
Density and relative density has many applications in everyday life, including the following:
1. It aids in the identification of gemstones such as gold and diamond.
2. Density is used by geologists and mineralogists to determine the mineral content of a rock or other sample.
3. Density is considered during the selection of building materials.
4. Density is also considered during the design of swimming and diving equipment.
5. Density is considered during design of various marine and air vessels so that they can float. For example, aeroplanes are made up of aluminium alloys and not steel. This is because the density of aluminium is less than that of steel, thus, it is lighter than steel. Moreover, aluminium is resistant to corrosion thus ensuring safety to the aeroplane and passengers. Figure 4.10, shows an aeroplane made of less dense material flying in the air.
6. Relative density can be used in determining the density of an unknown substance using the known density of another substance.
Chapter summary
1. Density of a substance is expressed as the mass of the substance per unit volume. Its SI unit is the kilogram per cubic metre, kg/m3. It can be expressed mathematically as ρ=m/v
2. The determination of the density of a solid depends on the shape of a particular solid. That is, whether the solid has a regular or irregular shape.
3. The density of solids is generally higher than the density of liquids. ⋅
4. Relative density of a substance is the ratio of the substance’s density to the density of water. It has no units since it is a ratio of the same quantity.
5. A relative density bottle is used to determine relative density of liquids.
6. Density is used in designing various structures for ships and aircraft.
7. Density is considered during the selection of building materials and design of swimming equipment.
Revision Exercise
Section A
1. Choose the most correct answer.
(i) A group of Form One students conducted an experiment to determine the density of wood. They measure the masses and volumes of different sized samples of a type of wood. Furthermore, they plotted the graph based on the data collected shown in Figure 4.11. Which graph depicts their results?

(ii) What is the density of the liquid in Figure below?

a) 0.5 g/cm3. (b) 2.0 g/cm3. (c) 8.0 g/cm3. (d) 10.0 g/cm3.
(iii) Two cylinders are made of the same metal shown in Figure 4.13. Both cylinders have the same cross sectional area but one is longer than the other. Which quantity is the same for both cylinders?
































Leave a Reply