Similarity - Topic 6: Mathematics Study Notes Form Two
Welcome to our website darsahuru.ac.tz, in this article, Are you looking for Topic 6: Similarity - Mathematics Study Notes Form II, Similarity Mathematics Notes, PDF Download Similarity Notes, Form Two Mathematics Notes, Mathematics Form II Study Notes
Similarity
Similar Figures
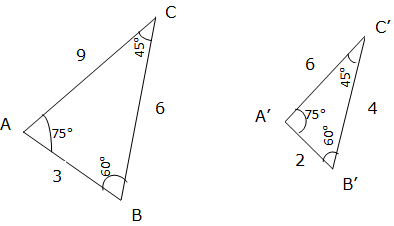
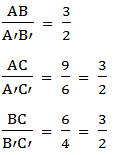
Since all sides have the same ratio i.e. they are proportional and the corresponding angles are equal i.e. angle A = angle A’, angle B = angle B’ and angle C = angle C’, then the two figures are similar. The symbol for similarity is ‘∼‘

(Equal Angles have been marked with the same number of Arcs)
- All their angles equal
- Corresponding sides have the same ratio
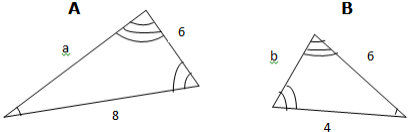
For example; Given similar triangles below, find the length of sides a and b


How to find if Triangles are Similar
- All their equals are angles
- The corresponding sides are in the same ratio
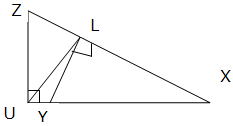
Intercept theorem
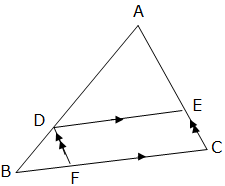
The Triangles ADE and BD have exactly equal angles and so they are similar (recall that the two Triangles are similar by AA).
1. AA (Angle-Angle):
this means, Triangles have two of their Angles equal. See an illustration below
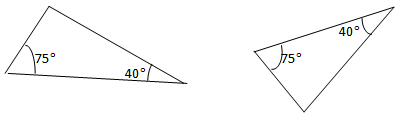
If two of their Angles are equal then the third Angle must also be equal, because Angles of a Triangle add up to1800. In our case, our third Angle will be:
2. SAS (Side-Angle-Side):
Means we have two Triangles where:
- The ratio between two sides is the same as the ratio between the other two sides
- The included Angles are equal

From our example, we see that, the side AB corresponds to side XZ and side BC corresponds to side YZ, thus the ratios will be:
3. SSS (Side-Side-Side):
Means we have three pairs of sides in the same ratio. Then the Triangles are Similar. For example;

In this example; the ratios of sides are:
a:x = 6:7.5 = 12:15 = 4:5
c:y = 4:5
b:z = 8:10 = 4:5
The ratios are all equal, so the Triangles are Similar.
Exercise 1
1. Use similarity to calculate side AB
2. ABC is a Triangle in which AC is produced to E and AB is Produced to D such that DE//BC. Show that AD:AB = DE:CB