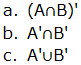Sets - Topic 10: Mathematics Study Notes Form Two
Welcome to our website darasahuru.co.tz, in this website you will find Topic 10: Sets - Mathematics Study Notes Form II, Form Two Sets Notes, Mathematics Notes PDF, Mathematics Notes For Form Two Free Download PDF.
Sets
This is where mathematics starts. Instead of mathematics with numbers we will think about mathematics with things.
The word set means collection of related things or objects. Or, things grouped together with a certain property in common. For example, the items you wear: shoes, socks, hat, shirt, pants and so on.
This is called a set. A set notation is simple, we just list each element or member (element and member are the same thing), separated by comma, and then put some curly brackets around the whole thing.
See an example below:
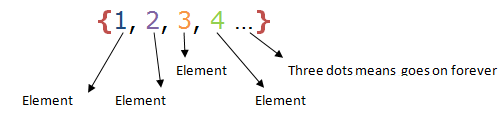
Sets are named by capital letters. For example; A = {1, 2, 3, 4 …} and not a = {1, 2, 3, 4, …}.
Description of a Set
We describe sets either by using words, by listing or by Formula. For example if set A is a set of even numbers, we can describe it as follows:
- By using words: A = {even numbers}
- By listing: A = {2, 4, 6, 8, 10,…}
- By Formula: A = {x: x = 2n, where n = 1,2,3,…} and is read as A is a set of all x such that x is an even number.
Example 1
Example 2
Write the following set in words: W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
The Members of a Set
List the members of a set
A set should satisfy the following:
- The members of the set should be distinct. (not be repeated)
- The members of the set should be well-defined. (well-explained)
- A={x: x is an odd number <10}
- B={days of the week which begin with letter S}
- C={prime numbers less than 13}
Naming a Set
To describe a small set, we list its members between curly brackets {, }:
- {2, 4, 6, 8}
- { England, France, Iran, Singapore, New Zealand }
- { David Beckham } {}
- (the empty set, also written ∅)
We write a ∈ X to express that a is a member of the set X. For example 4 ∈ {2, 4, 6, 8}. a /∈ X means a is not a member of X.
By listing: A = {2, 4, 6, 8, 10,…}
Types of Sets
Universal set
Empty set or Null set: is a set with no elements. There aren’t any elements in it. Not one. Zero elements. For example; A set of Countries South of the South Pole.
Infinite set: this is a set whereby we cannot count the number of elements of the set.
The Difference Between Equivalent and Equal Sets
Distinguish between equivalent and equal sets
Equivalent sets:
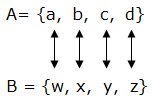
Generally, two sets are equivalent if n(A) = n(B). Symbolically we write A ≡B which means A is equivalent to B.
Equal sets:
Subsets
A Subset
Define a subset
Subsets of a Given Set
List subsets of a given set
If every element in A is also in B, and there exist at least one element in B that is not in A, we say that A is Proper subset of B.
And if every element in A is in B, and there is no element in B that is not in A, we say that A is an improper subset of B and we write A = B or symbolically we write A⊆B or B⊆A.
Consider an example below:
Operations With Sets
Union of Two Sets
Find union of two sets
The Compliment of a Set
Find the compliment of a set
Complement means ‘everything that is not’. For example; if A is a subset of a universal set, the elements of a universal set that are not in A are the complements of set A. complement of a set is denoted by C. So complement of set A is written as Ac. Or A′.
Inters ection
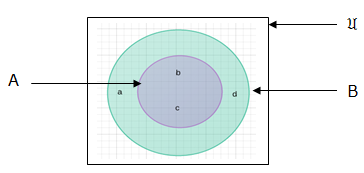
Vein Diagrams
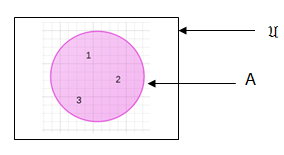
is a universal set which can be a set of counting numbers and A is a subset of it.
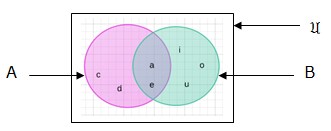
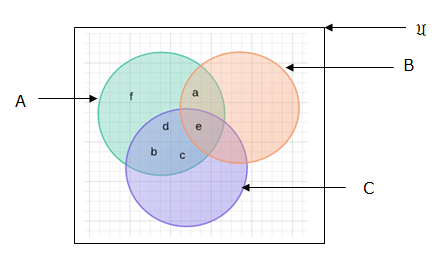
Example 2:
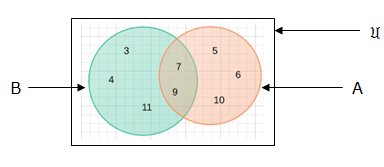
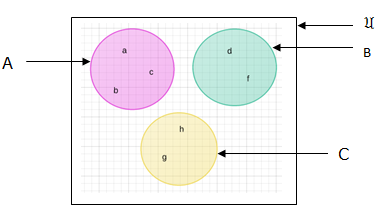
A = {a,b,c,d,e,f}, B = {a,e} and C = {b,c,e,d}. Represent in venn diagrams A∪B∪C and A∩B ∩C.
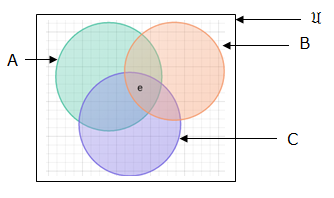
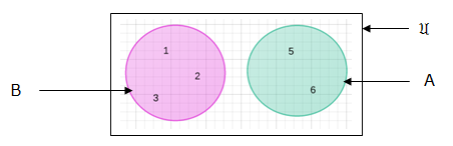
sets with no elements in common:
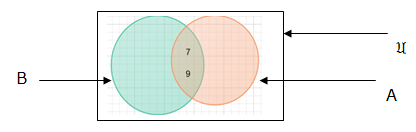
Number of elements in two sets say set A and B i.e. n(A∪B) is given by: n(A∪B) = n(A) + n(B) – n(A ∩B)
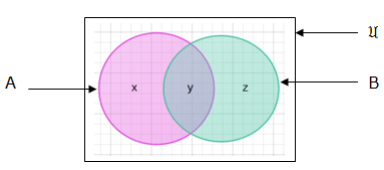
From our venn diagram:
Therefore, n(B) = 12
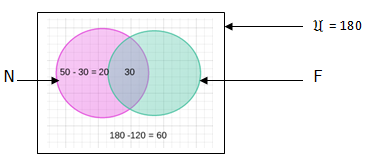
Word problems
- likes football.
- Likes neither of the sport
Solutions.
Thus,
n(F) = ?
n(F) only = 120 – 30 -20 = 70
Exercise 1
3. Which of the following sets are finite, infinite or empty sets.
A = {y:y is an odd number}
B = {1,3,7,…35}
C = { }
D = {Maths, Biology, Physics, Chemistry}
E = {Prime numbers between 31 and 37}
F = {….-2,-1,0,1,2,…}
- A⊂B
- B⊂A
- A⊆C
- C⊆B
5. How many subsets are there in set A = {f,g,I,k,m,n}? List them all.
- n(A∪ B)
- n(B) only.
- n(A) only.