Congruence - Topic 5: Mathematics Notes Form Two
Welcome to our website darasahuru.ac.tz, in this article, are you looking for Topic 5: Congruence - Mathematics Notes Form Two, PDF Notes Congruence, Notes Form Congruence, Mathematics Notes For Form Two, PDF Free Download Congruence, Form Two Mathematics Notes All topics, Congruence
Congruence
Note that; the two shapes need to be the size to be Congruent i.e. only rotation, reflection and/ or translation is needed.
Remember this:
- Two line segments are Congruent if they have the same length.
- Two angles are Congruent if they have the same measure.
- Two circles are Congruent if they have the same diameter.
Angles formed by the intersection of two straight lines
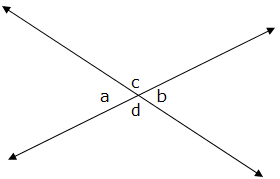
- They are Congruent: vertical angles are always of equal measure i.e. a = b, and c = d.
- Sum of vertical angles (all four angles) is 3600 i.e. a + b + c + d =3600
- Sum of Adjacent angles (angles from each pair) is 1800 i.e. a + d =1800 ; a + c =1800 ; c + b =1800 ; b + d =1800.
Congruence of Triangles
Two Triangles are Congruent if their corresponding sides are equal in length and their corresponding angles are equal in size. The symbol for congruent shapes is ≅
The Conditions for Congruence of Triangles
Determine the conditions for congruence of triangles
The following are conditions for two Triangles to be Congruent:
SSS (side-Side-Side): if three pairs of sides of two Triangles are equal in length, then the Triangles are Congruent. Consider example below showing two Triangles with equal lengths of the corresponding sides.
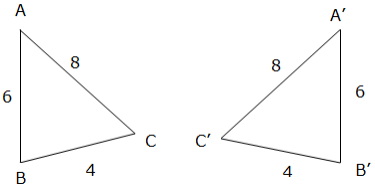
Example 1
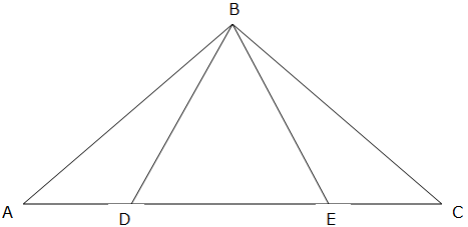
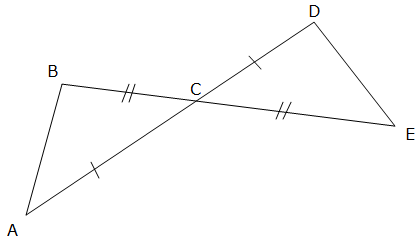
Prove that the two Triangles (ΔABC and ΔBCD) below are Congruent.
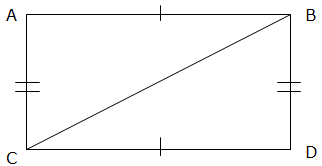

SAS (Side-Angle-Side): This means that we have two Triangles where we know two sides and the included angles are equal. For example;
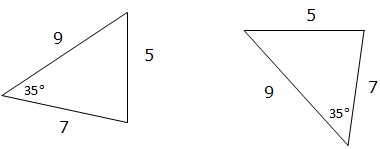
ASA (Angle- Side-Angle): If two angles and the included side of one Triangle are equal to the two angles and included side of another Triangle we say that the two Triangles are congruence. For example
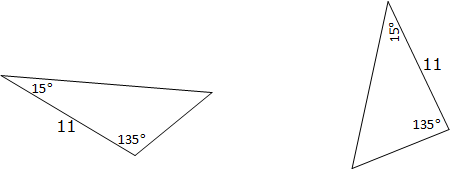
AAS (Angle-Angle-Side): If two angles and non included side of one triangle are equal to the corresponding angles and non included side of the other Triangle, then the two triangles are congruent. For example
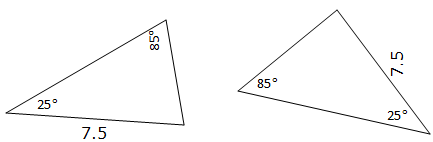
HL (hypotenuse-Leg): This is applicable only to a right angled triangle. The longest side of a right angled triangle is called hypotenuse and the other two sides are legs.
- The same length of hypotenuse and
- The same length for one of the other two legs.

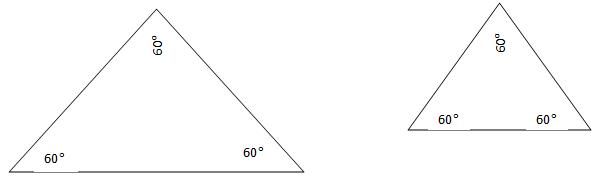
The two triangles are not congruent.
Without knowing at least one side, we can’t be sure that the triangles are congruent.
Congruence of Triangle
Example 2
Prove that the two Triangles (ΔABC and ΔBCD) below are Congruent.


Theorems on Congruence of Triangles to Solve Related Problems
Apply theorems on congruence of triangles to solve related problems
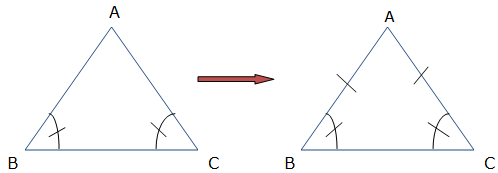
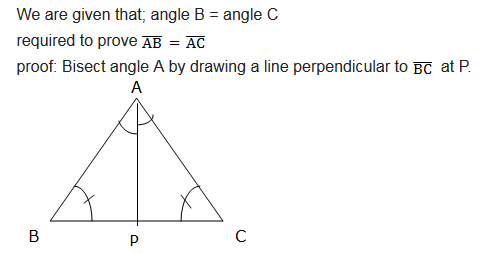
Isosceles Triangle Theorem
The figure below illustrates an example of an isosceles triangle:
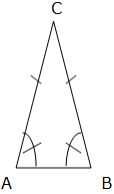
An isosceles triangle has two congruent sides (opposite sides) and two congruent angles. The congruent angles are called base angles and the other angle is called vertex angle. The angles A and B are base angles and angle C is the vertex angle.
The base angle Theorem
If two sides of a triangle are congruent, then the angles opposite to these sides are congruent
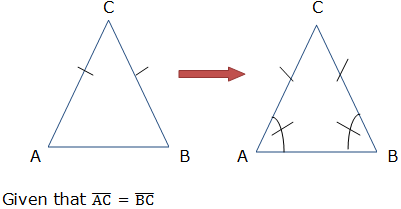

Therefore, the base angles i.e. angle CAS and angle BCS are equal (by the definition of a congruence of triangles).
It states that, if two angles of a triangle are congruent, then sides opposite those angles are congruent.