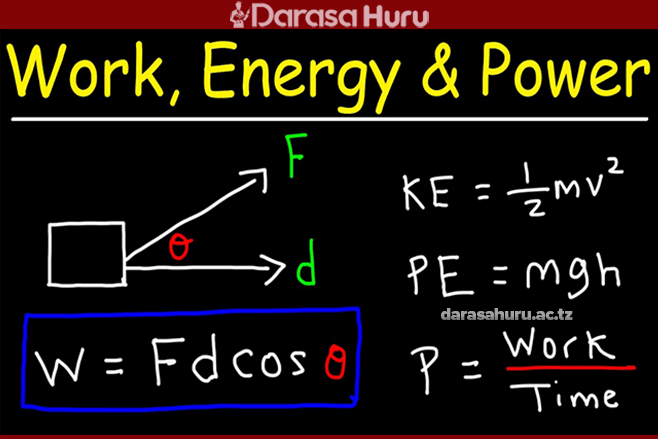
Work, Energy and Power – Physics Form One Notes
The terms ‘work’, ‘energy’ and ‘power’ are frequently used in everyday life. A farmer ploughing the field, a construction worker carrying bricks, a student studying for a competitive examination, and an artist painting a beautiful landscape, are all said to be doing work.
In physics, the word ‘work’ covers a definite and precise meaning, and so does energy and power. In this lesson, the concepts of work, energy and power will be discussed. The competencies developed will enable you to perform various tasks in different contexts.
Concept of work
In everyday life, the term work means any activity in which effort (either mental or physical) is exerted. However, in physics, work is done when a force acts on a body and the body moves in the direction of the applied force. The work done is measured by the product of the applied force and the distance moved by a body in the direction of the applied force.
Suppose, a force F is applied to push a block resting on a table. If the block moves through a distance d in the direction of the applied force, as shown in Figure 9.1, the work is said to be done.

Illustration of work done
Then, Work done (W) = force(F) × distance (d)
Therefore, W = Fd.
The SI unit of work is joule (J) which is equivalent to newton metre (Nm).
One joule is defined as the work done when a force of one Newton (N) moves an object through a distance of one metre in the direction of the force.
Other units used for measuring work are:
1 kilojoule (kJ) = 1 000 joules (J) and 1 Megajoule (MJ) = 1 000 000 J.
From the Physics point of view, work is specifically meant to describe what is accomplished by the action of a force that makes an object move through a certain distance in the direction of the force.
For example, a girl does work by lifting up books from the floor, as shown in Figure 9.2 (a). But in Figure 9.2 (b), the girl is pushing a wall which is not moving and hence, no work is done by pushing the wall because there is no distance moved in the direction of the push.


llustration of work
For example, if a boy applies a force of 3 N on a box and the box is pushed through a distance of 1.5 m, work is done on the box. The magnitude of this work is 4.5 J. Lifting a bag onto your head and lifting the books from the floor are examples of work, since, there is a distance moved in the direction of force. Thus, there are two conditions for work to be done.
1. There must be a force acting on an object.
2. The object must move along the direction of the applied force.
These conditions are illustrated in Figure



Illustration of the conditions for the work to be done
(a) If an object is lifted or lowered shown in Figure 9.3 (a), a vertical force is exerted on the object and it moves parallel to the force so work is done.
(b) If an object is simply held in the air shown in Figure 9.3 (b), an upward force is exerted on the object but the object is not moving. Thus, no work is done.
(c) If an object is held while walking across the room as displayed in Figure 9.3 (c), an upward force is exerted on it and the object is moving. However, the movement is not parallel to the force, no work is done.
(d) If the force and distance moved by the object are in opposite directions, work is done by the force.
(e) If the force and distance moved are at some angle, work is done only by the component of the force that is parallel to the distance moved.
(f) If the force and distance moved are perpendicular (at a right angle) to each other, no work is done.
Example 1
A force of 80 N pulls a box along a smooth and level ground through a distance of 5 m. Calculate the work done by the force.

Solution
Force (F) = 80 N, distance (d) = 5 m, work done (W) is given as:
W = F × d
= 80 N × 5 m
= 400 J
Therefore, the work done is 400J.
Example 2
How much work is done in lifting a 7 kg object through a height of 2 m and then holding it at that height for 10 s? (Assume, g = 10 N/kg)

Solution
Mass (m) = 7 kg, distance (d) = 2 m, g = 10 N/kg
To lift an object or hold it in the air, an upward force equal to its weight must be exerted.
Weight (N) of an object = mass (kg) of an object × acceleration due to gravity (N/kg)
w = mg
But, weight = Force
Then,
Force = mg = 7 kg × 10 N/kg = 70 N
So, you must exert on the object an upward force of 70 N.
To lift the object a distance of 2 m, the work done is calculated as follows:
W = F × d
= 70 N × 2 m
= 140 J
To hold the object for 10 s:
F = 70 N, d = 0 m
W = F × d
= 70 N × 0 m
= 0 J
So, 140 J of work was required to lift the object at a height of 2 m, but no additional work was done in holding the object at that height for 10s.
Exercise 1
Answer all questions (where necessary use g = 10 N/kg).
1. If a man pushes a van with a force of 300 N for a distance of 10 m, how much work does he do?
2. A man lifts a load of 20 kg through a height of 3 m. Calculate the work done.
3. Zenge lifts a brick of mass 10 kg from the floor to a shelf that is 3 m high. How much work does she do?
4. In each of the following cases, state whether work is done or not.
(a) A cow pulling a 50 kg cart of maize along a rough road.
(b) A teacher holding a book in his hand while talking to his friend.
(c) An aeroplane flying upward at take-off.
(d) An aeroplane moving horizontally 3 000 m above sea level
5. A sack of rice which weighs 900 N is lifted to a height of 2 m. Calculate the work done against gravity.
Concept of energy
Energy plays a role in our daily activities, such as cooking, freezing, lighting, and manufacturing. In science and engineering, energy is defined as the ability to perform work. An object possessing energy can do work and transfer that energy to another object, enabling it to perform work as well. In essence, energy quantifies an object’s capacity to do work.
Thus, energy is referred to as the ability to do work.
To understand the concept of energy, imagine a person driving a nail into wood, as shown in Figure below. When the hammer is lifted, it gains energy. When the raised hammer strikes the nail, the energy from the hammer is transferred to the nail, driving it into the wood.

Driving a nail into wood
Since work is done when energy is available, the SI unit of energy is the same as that of work, that is, joule (J). One joule of energy is the energy required to do one joule of work. Sometimes energy is expressed using a larger unit of energy called kilojoule (kJ) such that 1 kJ equals to 1000 J.
Forms of energy
Energy exists in different forms, including mechanical energy, chemical energy, electrical energy, heat energy, light energy, sound energy and nuclear energy. One form of energy can be converted into another form, as illustrated in Figure below:

Forms of energy
Mechanical energy is the energy possessed by an object due to its position or motion. The mechanical energy due to the position of the object is referred to as the potential energy (PE). Meanwhile, the mechanical energy due to the motion of the objects is known as kinetic energy (KE).
Electrical energy is due to the kinetic energy of the moving electric charges in a circuit. Electric charges pose energy due to their position. This energy is known as the electric potential energy and is determined by the electric forces between the charges.
Devices such as batteries store energy in form of the electric potential energy. That is, when a battery is charged it stores the electric potential energy so that it can be used later. Figure 9.6 shows some batteries connected to an electric bulb converting stored electrical energy into light.

Battery powering an electric bulb
Heat or thermal energy is the energy that comes from the movement of particles within a substance. As particles move and collide, they generate heat, which is a measure of thermal energy. The faster the particles move, the higher the thermal energy and, consequently, the temperature of the substance.
Thermal energy can be transferred between objects through conduction, convection, or radiation. It plays a crucial role in everyday processes, from cooking food to powering engines and regulating climate. Thermal energy is useful in cooking as shown in Figure.

Thermal energy from natural gas
Nuclear energy comes from the potential energy possessed by the constituents of an atomic nucleus. The nuclear constituents are subject to both strong and weak nuclear forces and have nuclear potential energy. Nuclear energy can be released during nuclear reactions and radioactive decay.
Nuclear reactions involve nuclear fission and fusion. These reactions can be made to occur in a special facility called a nuclear reactor. A sketch of a nuclear reactor is shown in Figure

Nuclear reactor
Electromagnetic energy (infrared radiation, visible radiation, ultraviolet radiation, and so on) is associated with accelerating electric charge, and therefore with the changing velocity of that charge or oscillating electric and magnetic fields.
Radiant light energy is the most common form of electromagnetic energy. The sun provides radiant energy to the earth as shown in Figure

Radiant energy from the sun
Sound energy is also a form of energy that is transferred in the form of waves arising from the vibration of a membrane and mechanical oscillations. Sources of sound may be speakers, sound boxes, and vibrations from the wings of insects.
A microphone converts sound energy into an electrical signal and a loudspeaker converts electrical energy into sound energy. Figure 9.10 shows an example of a loudspeaker.

Kinetic and potential energy
Potential and kinetic energy are due to the position and motion of an object, respectively. In this section, you will learn about kinetic energy and potential energy.
Kinetic energy
This is the energy possessed by an object due to its motion.
Any matter that is moving has kinetic energy. Both a plane flying through the air and an atom vibrating in a solid have kinetic energy. Consider a 7-tones lorry and a 1 tone mini vehicle both travelling at a speed of 80 km/hr.
In case of an accident, one expects the lorry to cause more damage than the mini vehicle. This is because the lorry possesses higher kinetic energy than the mini vehicle. The kinetic energy of an object depends on its mass and speed. For a body of mass m travelling at speed v, its kinetic energy (KE) is expressed as:
KE=1/2mv2
The SI unit of kinetic energy is Joule (J) which is equivalent to kgm2 /s2 . When the velocity of a body increases or decreases, its kinetic energy changes. Consider an object of mass m initially moving with speed u and attains the final speed v.
The corresponding change in kinetic energy (ΔKE) is given as the difference between the object’s final kinetic energy and initial kinetic energy. That is:
ΔKE = KEfinal − KEinitial
= 1/2mv2 – 1/2mu2
ΔKE=1/2m(v2−u2).
Example 3
An object has a mass of 5 kg. What is its kinetic energy if its speed is:
(a) 5 m/s?
(b) 10 m/s?

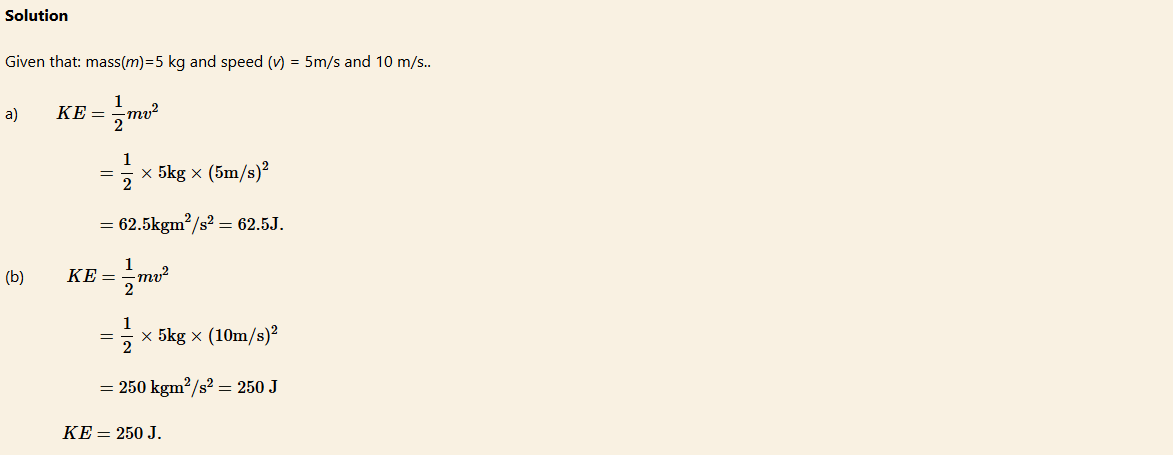
Comparing the two examples, it shows that, if the speed of an object is doubled, its kinetic energy increases by a factor of 4.
Example 4
What is the kinetic energy of a 12 g bullet travelling at the speed of 320 m/s?

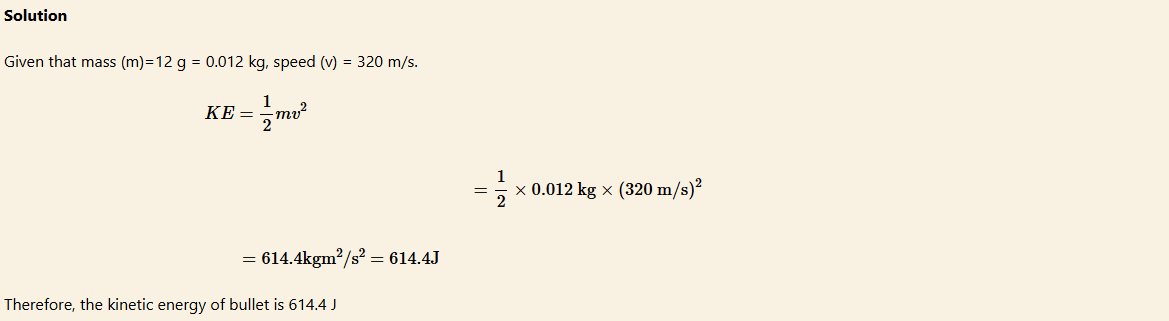
Activity 1
Aim: To investigate the relationship between work and kinetic energy.
Materials: Wooden block, PVC tube, metre rule and metal ball
Procedure
1. Place one end of a PVC tube about 1 m long on a wall while the other end rests on a smooth table.
2. Using a metre rule measure perpendicular height (h) from the table to the point where the PVC tube rests on the wall. Record the value of h (start with h = 100 cm).
3. Place the wooden block as shown in Figure

4. Release the metal ball from the upper end of the wall, so it rolls inside the tube towards the lower end.
5. Using a metre rule measure and record the distances (d) that the wooden block moves as it is pushed by the rolling metal ball.
6. Repeat steps 2 to 5 for the values of h = 80 cm, 60 cm, 40 cm and 20 cm. Record your results as in Table
7. Plot a graph of distance d (cm) against the height h (cm).
Questions
(a) Discuss how the height of the raised end of the tube and the distance that the wooden block is pushed are related.
(b) what would be the effect of the ball’s mass on the distance travelled by the ball if the height is kept constant? Explain your answer.

A walking elephant in Figure below has high kinetic energy because of its large mass. If one collides with a walking elephant, part of its kinetic energy can be transferred to the person, resulting in serious injuries.

A walking elephant
Potential energy
Potential energy is the energy possessed by an object due to its position.
An object can have potential energy if it is acted upon by a restoring force that tends to restore it to its initial position after it has been displaced. For example, a body raised from the ground to a certain height has gravitational potential energy due to gravitational force.
On release, it returns to the ground, thus its potential energy relative to the ground becomes zero. Another type of potential energy is due to elastic force in a compressed spring (Figure below). This is elastic potential energy.

Compressing spring
Several restoring forces lead to various types of potential energies. Two types of potential energy are briefly discussed here.
Elastic potential energy
This is the energy stored in objects like springs as a result of reversible deformation. When a force is applied to a spring, it gets compressed or stretched. But when the force is removed, it regains its original shape and size. In the deformed state, the spring has elastic potential energy.
When the elastic material is being stretched through a distance x (Figure below), work is done on the material. This work is stored as potential energy in the spring. This fact can be verified through the force versus extension graph for the spring. The area under the curve in the force-extension graph gives the elastic potential energy stored in the spring.

Force-extension graph
According to the Hooke’s law:
Force (F) = spring constant (k) × extension (x)
F = kx
The area under the force-extension graph represents the work done in stretching or compressing the elastic materials. The energy stored in the stretched spring is an elastic potential energy.
The area under the curve = Area of the shaded region of the curve

Gravitational potential energy
Suppose a force F is used to lift an object with a mass (m) from an initial height (hi) to a final height (hf) at a constant velocity, as described in Figure 9.15. Since the object moves in the direction of the force, work is done on the object.

An object is lifted from hi to hf
The force required to lift an object at a constant velocity has a magnitude equal to the object’s weight, mg.
F = mg.
Multiplying both sides by the displacement (d) gives:
Fd=mgd.
The displacement of the object is equal to the change in its height as shown in Figure 9.15. Thus,
d = hf − hi
Substituting this expression on the right side of the above equation gives:
Fd = mg(hf – hi)
Fd = mghf − mghi .
The quantity on the left side of the equation is the work done. The quantities, mghi and mghf are the respective potential energy values at the heights hi and hf. The difference between mghi and mghf is the change in the object’s PE. It follows that, change in potential energy is equal to work done (W) in lifting the object that is ΔPE = W.
If hi = 0, that is the ground level is the reference level, then
PE = mgh
where h is the height from the surface.
Thus, PE = mgh.
When determining the PE of an object, a reference level from which h is measured must be chosen. The choice is arbitrary and the reference level can be located anywhere. For convenience, the reference level hi is considered to have zero PE. Note that, while the PE of an object depends on the location of the reference level, the change in PE does not. The SI unit of PE is Joules which is equivalent to (kgm2/s2) just like KE.
PE depends on mass, acceleration due to gravity and height of an object above a reference level as opposed to KE which is dependent on mass and velocity. When a force lifts an object at a constant velocity, the work done by the force equals the change in the object’s gravitational potential energy. That is, PE = W = mgh.
Example 5
A stone of 2 kg mass falls from a height of 25 m above the ground. Calculate the PE initially possessed by the stone.

Solution.
m = 2 kg, g = 10 m/s2
PE = mgh
=2kg×10m/s2×25m
=500kgm2/s2=500J
Therefore, PE of the stone is 500 J.
Example 6
A 2 kg object is at rest on a table 1.2 m above the floor. The ceiling in the room is 2.8 m above the floor as shown in Figure

(a) What is the gravitational potential energy of the object relative to;
(i) the table top?
(ii) the floor?
(b) Find the work done in lifting the object from the top of the table to the ceiling.
Solution
(a) Gravitational potential energy
(i) At the table top
h = 0,
PE = mgh
= 2 kg × 10 m/s × 0 m = 0 J
(ii) Relative to the floor
h = 1.2 m,
PE = mgh
=2kg×10m/s2×1.2m
=24J
(b) d = 2.8 m − 1.2 m = 1.6 m
But ΔPE = mgh
=2kg×10m/s2×(1.6m)
=32J
Therefore, the work done = 32 J.
Example 7
Find the elastic potential energy stored in the spring with k = 50 N/m when the spring is compressed by 0.2 m.
Solution.
Given: k = 50 N/m and x = 0.2m
Now, elastic potential energy stored in the spring is given by,
12kx2
Plugging the values in the above formula,
PE=12kx2
PE=12×(50N/m)×(0.2m)2=1J
Therefore, PE = 1J
Example 8
Find the elastic potential energy stored in the spring with k = 100 N/m when the spring is compressed by 0.1m.

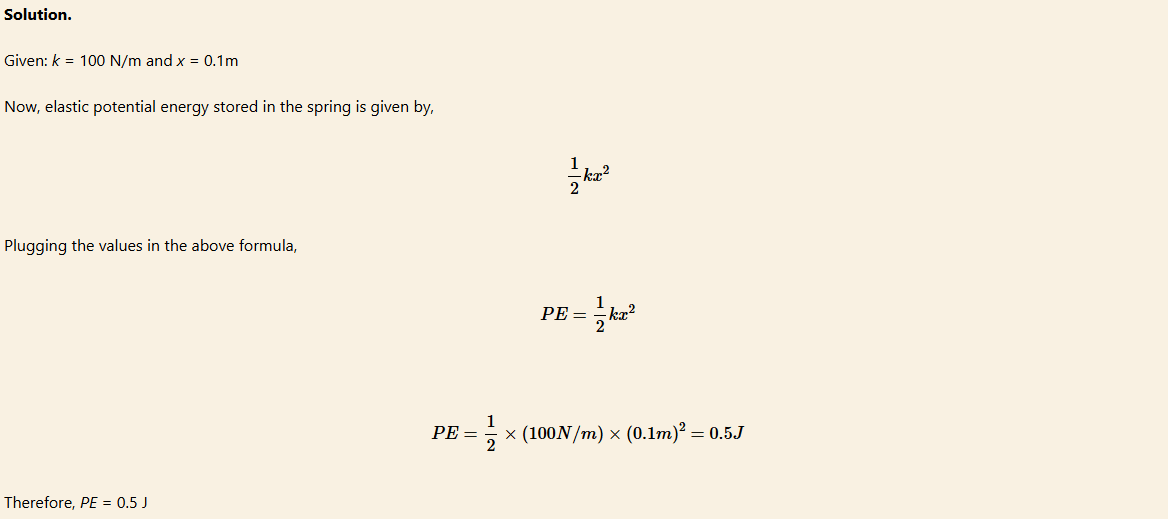
Exercise 2
Answer all questions (where necessary use g = 10 N/kg).
1. State five forms of energy.
2. (a) Determine the potential energy possessed by a particle of mass 0.2 kg resting on a tabletop 1.6 m above the floor.
(b) Amina has a mass of 80 kg. If she runs at a speed of 10 m/s, calculate her kinetic energy.
3. A stone of mass 10 kg is dropped down to the ground from the roof of a building 20 m high. If it hits the ground with a velocity of 20 m/s, determine its:
(a) kinetic energy.
(b) change in potential energy.
4. Find the elastic potential energy stored in the spring with k = 100 N/m when the spring is stretched to 0.5m from its natural length of 1 m.
5. A spring with spring constant k = 100 N/m was initially compressed by x = 0.4 m, after that, it was released and stopped at x = 0.2 m compression. Find the work done by the restoring force in this process.
Activity 2
Aim: To demonstrate the existence of potential energy and kinetic energy.
Materials: Helical spring, thread, retort stand, and 100 g mass
Procedure
1. Clamp a helical spring on a retort stand.
2. Attach a 100 g mass to the bottom of the spring.
3. Pull the mass downward for about 5 cm then release it.
4. Observe the up and down motion of the mass.
Questions
(a) What form of energy did the mass have at the initial rest point?
(b) Explain the changes in energy as the mass moves up and down.

When a helical spring is set in motion, the mass possesses kinetic energy. Initially, it had potential energy due to its position. A mass at rest possesses potential energy only.
Task 1
1. List down all forms of energy that you know.
2. Discuss and illustrate the importance of the forms of energies you have listed.
Transformation of energy
Energy provides a capacity to do work. Different types of work require different forms of energy. Therefore, energy can be transformed from one form to another. The transformation of energy is referred as energy conversion. Transformation of energy occurs everywhere and every second of the day. However, during the energy transformation, the total amount of energy remains constant.
Consider the example of a raised hammer striking a nail described in Figure 9.4. As the hammer strikes the nail it does work, energy is converted from potential energy to kinetic energy. When the brick hits the nail, parts of the energy is used to drive the nail while some energy are converted to heat and sound energies. Figure 9.17 shows the relationship between work and energy.

Work and energy are interchangeable
Note that; for any useful work to be done, energy is required. Cooking gas, petrol, and food store chemical energy which can only be used after changing it into other forms of energy through a chemical reaction.
For example, a car is fuelled at a petrol station as shown in Figure 9.18 before it can be driven. Chemical energy stored in petrol is eventually converted into mechanical energy, thus enabling the car to move.

Consider a locomotive diesel engine such as a train shown in Figure below. The fuel is burnt to release chemical energy which is in turn converted to mechanical rotational energy. This rotation is transferred to the wheels and makes the train move.

Train that uses diesel engine
When a stone drops from a cliff of height, h, its PE decreases while its KE increases as it falls. On hitting the ground, some dust may fly off (KE) and some sound may be heard (sound energy). The point of impact may also become warmer as a result of the impact. This shows that, PE has been converted into heat energy. The energy changes are as follows:
PE → KE → KE + sound energy + heat.
Note that; although energy is transformed from one form to another, it is never used up or lost.
Other examples of situations where energy is transformed are as follows:
1. Water at the top of a dam has potential energy. This is transformed into kinetic energy as the waterfalls.
2. The PE of a stretched bow can be transformed into KE of an arrow.
3. Consider a footballer kicking a ball. The chemical energy in his muscles is converted into the kinetic energy of the ball which partly changes into heat energy.
Principle of conservation of energy
Suppose a 3 kg object is dropped from a height of 5 m above the ground as in Figure 9.20. Ignoring the effects of air resistance, the object will fall to the ground with an acceleration due to gravity, g.
Choosing the ground as the reference level, the PE of the object when released is:
PEi = mgH
= 3 kg × 10 N/kg × 5 m
= 150 J
= 150 J

Since its initial velocity was zero, it had no KE when released, KEi = 0.
Upon reaching the ground, it had no PE. Since hf = 0, PEf = 0. It does however has kinetic energy. Therefore, kinetic energy, KEf = 150 J.
Note: KE = PE = 150 J. Since no energy is lost, the final velocity can always be calculated.
This means that while falling under the influence of gravity, the initial PE of the object is completely converted into kinetic energy as it falls. This illustrates the principle of conservation of energy which states that:
“Energy is neither created nor destroyed but can be transformed from one form to another.”
One can verify this principle by determining the total mechanical energy at each stage of falling objects.
At the point of release, the object has potential energy but zero kinetic energy. Thus, the total mechanical energy at this stage is = KE + PE = 0 J + 150 J = 150 J
When the object is at halfway to the ground (hf = 2.5 m).
The final PE and KE are:
PEf = mgh
= 3 kg × 10 N/kg × 2.5 m
= 75 J
KE = E − mgh
= KE = 150 J − 75 J = 75 J.
One half of the initial PE has been converted to KE.
The total mechanical energy, E, of an object is the sum of its potential and kinetic energies.
E = KE + PE.
Thus, E = 75 J + 75 J = 150 J
When the object reaches the ground, the total energy is given as:
E = KE + PE = 150 J + 0 J = 150 J
So, while the object was falling its PE decreased and its KE increased. In this case, its total mechanical energy remained constant. The total mechanical energy was therefore conserved.
Conversion of energy can also be studied by considering the motion of a simple pendulum shown in Figure 9.21. A pendulum is a mass suspended by a string or wire from a fixed point so that it can move back and forth along an arc. The lowest point in its motion is called the equilibrium point and is usually considered as the reference point, shown in Figure 9.21 (a).
Two forces act on the pendulum. The force of gravity (weight) of the pendulum and tension T in the string. The tension does not work because it always acts along the string and is always perpendicular to the displacement (see Figure 9.21 (b)). Therefore, the total mechanical energy of the pendulum remains constant

Conservation of mechanical energy
At points A and D, where the pendulum reaches the highest points above the equilibrium point, the total energy is equal to PE. At Point C, the pendulum is at its lowest point.The total energy is equal to the KE. At points like B, between the highest and the lowest points, total energy is the sum of KE and PE.
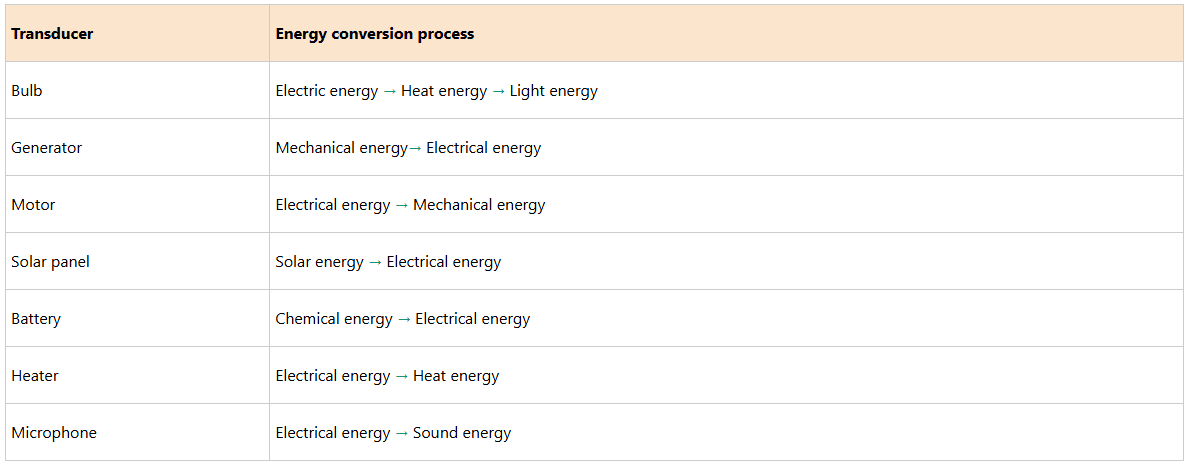
Transducer
A device used to convert one form of energy to another is called a transducer. Table 9.2 shows some transducers and the corresponding energy transformation.
Example 9
At its highest point A in Figure 9.22, a pendulum of mass 0.8 kg is 1.2 m above the equilibrium point. What will be its velocity as it swings through its lowest point?


Uses of mechanical energy
Mechanical energy enables objects to apply a force on other objects to cause displacement and hence do useful work. For a car, truck, train, or aeroplane to move, mechanical energy is needed. Electricity is normally obtained by dynamos which are driven by some forms of mechanical energy. Juicer uses mechanical energy to squeeze fruits.
Task 2
Discuss the role of mechanical energy in your daily life.
Task 3
Identify and discuss the energy changes in:
(a) Rotating fan.
(b) Wood splitting.
(c) Throwing up a stone.
(d) Burning of charcoal.
(e) Striking a tuning fork.
(f) Eating potatoes.
(g) Lighting a torch.
(h) Swimming.
Is the law of conservation of energy obeyed?
Concept of power
Imagine you are tasked to design an elevator system for a high-rise building. The elevator needs to lift a certain load, say 1,000 kg to a height of 50 m. If the elevator must complete the lift in 20 s, then you need to calculate the power required by the motor to perform this task efficiently. Power, in this context, is the rate at which work is done or energy is transferred. The faster the elevator needs to lift the load; the more power is required. This concept is crucial in engineering because it helps determine the appropriate specifications for motors, engines, and other machinery, ensuring they can perform tasks within the desired time frame without overloading or wasting energy.
Power is the rate at which work is done. It is a measure of the rate at which energy changes.
This means that whenever work is done, energy changes into a different form.
Power is measured in Joules per second (J/s) or Watts (W). 1W=1J/s.
Mathematically, power may be expressed as:

Therefore, a watt is defined as the power dissipated when one joule of work is done in one second.
Power may also be calculated using alternative formulae as presented in Table

Note: These alternative formulae may be used depending on the given situation.
Other units of power are: kilowatts (kW), horsepower (hp) and Megawatts (MW). Their equivalence to the Watt is:
1 kW = 1 000 W
1 MW = 1 000 000 W
1 hp = 746 W
Task 4
Compare the rate of doing work by two cranes; A and B, when each crane lifts a body of mass 200 kg through a distance of 20 m. Crane A lifts the body in 15s while crane B requires 20s to lift it.
Assuming the cranes lift the body at a constant velocity.
(a) Do they do the same work?
(b) Which crane has more power?
Example 10
A model of a car of mass 20 kg moves at a speed of 6 m/s for 10 s. Find the power developed by its engine.
(a) in watts.
(b) in horsepower.

Solution
a) Data given
Mass, m of the model car = 20 kg
Speed, v of the car = 6 m/s
Time, t taken = 10 s
Power, P is given by:

Running upstairs is another area where power is required. Running upstairs increases one’s gravitational potential energy by the same amount as walking up, Figurebelow. However, the energy transferred during running upstairs is at a higher rate. When you run upstairs, you dissipate more than when you decide to walk up.

Walking upstairs
Crossing water bodies is energy-draining because more power is required for an individual or animal to cross from one bank of a river to the other. Figure below shows an elephant crossing a river.

An elephant crossing a river
Example 11
How much power is required for a car of mass 1000 kg to change speed from 10 m/s to 40 m/s in 8 s?

Solution
The work done on the car increases its kinetic energy.

Since work causes a change in energy, power can also be considered as the rate of change of energy.

For example, a light bulb converts electrical energy into light and heat. A 60-Watt light bulb converts 60 J of electrical energy each second from electrical to light and heat energy.Most appliances have a rating plate on them showing exactly how many watts they use.
Activity 3
Aim: To determine the power developed by your legs.
Materials: A flight of stairs, weighing scale, stopwatch, and tape measure
Procedure
1. Measure your weight in Newtons and note it down.
2. Measure the vertical height of the stairs as in Figure

3. Record the height in metres.
4. Using a stopwatch, record the time taken to run from the bottom to the top of the stairs.
5. Other individuals can repeat step 4.
Questions
(a) Calculate the amount of work done.
(b) Calculate the power dissipated in running upstairs.
(c) Find out who developed the highest power.
Assume there are n stairs and the height of each stair is h cm. If your mass is m kg and runs upstairs in t seconds, then, the total work done is given by
Wtotal = mg(nh)

Example 12
A man whose mass is 80 kg walks up a flight of 25 steps each 20 cm high in 10 seconds. Find the power developed by the man in kilowatts.
Solution
Given data
Mass of the man (m) = 80 kg
Number of steps (n) = 25
Height of each step (h) = 20 cm = 0.2 m
Time taken (t) = 10 s

Exercise 3
Answer all questions
1. A forklift is used to raise a mass of 400 kg to a height of 2 m in 4 seconds. Determine the power developed.
2. A truck for transporting sand is filled to its capacity. The total mass of the sand was 5000 kg. If a digger had to climb through a height of 2 m 100 times to fill the truck, calculate:
(a) the work done in loading the truck; and
(b) the power developed if the digger took 5 seconds per climb.
3. If a crane lifts a load weighing 3000 N through a height of 10 m in 500 seconds, what is the power of the crane?
4. Convert the following
(a) 11 936 W into hp.
(b) 2.5 hp into W.
5. A body of mass 50 kg is raised to a height of 2 m above the ground.
(a) What is its potential energy?
(b) If the body falls down, find its kinetic energy:
(i) when halfway down.
(ii) just before impact with the ground.
Chapter summary
1. Work is done when a force acts on an object and the object moves in the direction of the force. Work is therefore the product of force and distance moved in the direction of the force. Work is measured in Joules.
2. Energy is the ability to do work and is also measured in Joules.
3. Mechanical energy consists of kinetic and potential energy.
4. Kinetic energy is the energy an object has due to its motion. KE=1/2mv2
5. Potential energy is the energy stored in an object or energy due to its position. PE = mgh
6. Power is the rate at which work is done. It is a measure of the rate at which energy changes. P = W/t
Revision Exercise
Section A
1. Choose the most correct answer.
(i) Work is said to be done when
(a) force acts upon a body, but the body does not move.
(b) force acts upon a body and it moves it in the direction of applied force.
(c) force acts upon a body but the body does not move in the direction of the force.
(d) force acts upon a body and the body moves in opposite to the direction of applied force.
(ii) A constant horizontal force F displaces a box by distance d over a rough horizontal surface. Study Figure

The normal force acting on the box does NO work on the box during the motion because it is
(a) equal to the applied force.
(b) perpendicular to the applied force.
(c) equal and opposite to the weight of the box.
(d) perpendicular to the displacement of the box.
(iii) The food consumed by a human being produces
(a) only kinetic energy.
(b) only heat energy.
(c) both heat energy and chemical energy.
(d) only chemical energy.
(iv) Work done and energy are related in that
(a) they are both a result of mechanical processes.
(b) they have the same unit in which they are measured.
(c) they all explain how fast a certain task is performed.
(d) all are typical examples of chemical energy.
(v) A student calculates his power in running up a flight of stairs. He measures the vertical height of the stairs, the time taken to run up the stairs and his weight. How does he calculate his power?

(vi) The table shows some data from a high jump competition. Which athlete jumps the highest?

(vii) A student is investigating the energy changes when a ball is dropped from a height. The Figure below illustrates the energy changes when a ball is released at three different positions.

Ignoring the effects of air resistance, which statement about the total energy of the ball is correct?
(a) It is the same at all points.
(b) It is greatest at point 1.
(c) It is greatest at point 2.
(d) It is greatest at point 3.
(viii) Which one of the following quantities has the same unit?
(a) speed and force.
(b) work done and energy.
(c) work done and power.
(d) potential energy and power.
(ix) The diagram shows a small car of mass 500 kg approaching a hill. It moves up the hill with constant speed as shown in Figure

The gravitational field strength g is 10 N/ kg. Ignoring friction, how much work is done in moving the car up the hill?
(a) 50 × 103 J
(b) 5.0 × 103 J
(c) 1.0 × 105 J
(d) 1.0 × 106 J
(x) Which one of the following equations shows the relationship between power and work done?

2. Match each item from Column A with its corresponding item in Column B. Then, write the letter of the correct response in the space provided.

Section B
3. (a) Define the term work.
(b) What happens to work done when force and displacement are in the same direction?
(c) What happens when force and displacement are in opposite directions?
4. (a) Define the term power.
(b) How is power measured?
(c) Express 6900 J/s in horsepower.
5. Explain why a rotating wonder wheel becomes hot after a sudden stop.
6. Calculate the work done in each case below. Indicate if the work is done on the object or by the object.
(a) A 10 kg object is lifted to a height of 5m above the ground.
(b) The object is held at a height of 5m for 7s.
(c) The object is lowered back to the ground.
7. A motor exerts a horizontal force of 200 N in pulling a box 10 m across a level floor. How much work does the motor do?
8. An object is dropped and falls to the ground. Is there any work done while it is falling? If so, what force is responsible? Is the work done on or by the object?
9. A 1 000 kg car is travelling down the road at a speed of 15 m/s. How much kinetic energy does it have?
10. A 1 000 kg car travelling at 15 m/s has its speed increased to 45 m/s. How much kinetic energy would it have? How many times greater is the kinetic energy at 45 m/s than at 15 m/s?
11. Rock A has a mass of 2 kg and a speed of 1 m/s. Rock B has a mass of 1 kg and a speed of 2 m/s. Which rock has more kinetic energy?
12. If your mass is 45 kg, how much work would you do in climbing a ladder that is 5 m high?
13. The total mass of a wheelbarrow and its load is 90 kg. A worker pushes the wheelbarrow and loads up a plank of length 2.0 m onto a platform. The platform is at a height of 0.65 m above the ground as shown in Figure

If the worker exerts a force of 300 N on the wheelbarrow in the direction in which the wheelbarrow moves.
(i) Calculate the gravitational potential energy gained by the wheelbarrow and its load.
(ii) Calculate the work done on the wheelbarrow by the worker, after moving by 2 m.
(iii) Suggest a reason as to why the answers in (i) and (ii) are different.
14. (a) Discuss the energy changes in a firework.
(b) A 3.00 kg object is lifted from the floor and placed on a shelf that is 2.50 m above the floor.
(i) What was the work done in lifting the object?
(ii) What is the gravitational potential energy of the object sitting on the shelf?
(iii) If the object falls off the shelf and falls to the floor, what will its velocity be when it hits the floor? ignore air resistance.
15. Which object has more kinetic energy between a 10 kg object travelling at 5 m/s and a 5 kg object travelling at 10 m/s?
16. How much work is required to stop a 1 500 kg car travelling at 20 m/s?
17. A 2 kg object is on a tabletop 1.1 m above the floor. How much work is required to lift it at a constant velocity to a shelf 1.3 m above the floor?
18. A 0.5 kg ball is dropped from a height of 2.3 m above the floor. If upon hitting the floor it loses 3 J of energy, how high will it bounce?
19. A 3 kg box starts sliding down a hill that is 3.3 m high with an initial velocity of 5 m/s. If on reaching the bottom of the hill its velocity is 7.5 m/s, how much work is done by the box to overcome friction?
20. A student pulls a spring with a spring constant k=120 N/m stretching it from its rest length of 0.10 m to 0.20 m. Determine the elastic potential energy stored in the spring.