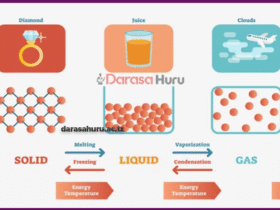
Radical Revision Questions Form Two Basic Mathematics
Radicals are opposite of exponents. For example when we raise 2 by 2 we get 4 but taking square root of 4 we get 2. The same way we can raise the number using any number is the same way we can have the root of that number. For example, square root, Cube root, fourth root, fifth roots and so on.
We can simplify radicals if the number has factor with root, but if the number has factors with no root then it is in its simplest form. In this chapter we are going to learn how to find the roots of the numbers and how to simplify radicals.
When a number is expressed as a product of equal factors, each of the factors is called the root of that number.
For example,25 = 5× 5;so, 5 is a square root of 25: 64 = 8× 8; 8 is a square root of 64: 216 = 6 ×6 ×6, 6 is a cube root of 216: 81 = 3 × 3 ×3 ×3,3 is a fourth root of 81: 1024 = 4 ×4 ×4 ×4 ×4, 4 is a fifth root of 1024.
Therefore, the nth root of a number is one of the n equal factors of that number. The symbol for nth root isn√ where √ is called a radical and n is the index (indicates the root you have to find).
If the index is 2, the symbol represents square root of a number and it is simply written as √ without the index 2.n√pis expressed in power form as,
![]()


































Leave a Reply