Pythagoras Theorem and Trigonometry Revision Questions Form Two Basic Mathematics
A. Pythagoras Theorem
Triangle with a Right angle i.e. 90° has an amazing property. Do you want to know what property is that? Go on, read our notes to see the amazing property of a right angled triangle.
Pythagoras Theorem deals only with problems involving any Triangle having one of its Angles with 900. This kind of a Triangle is called Right angled triangle.
When triangle is a right angled triangle, squares can be made on each of the three sides. See illustration below:

The Area of the biggest square is exact the same as the sum of the other two squares put together. This is what is called Pythagoras theorem and it is written as:

that is:

‘c’ is the Longest side of the Triangle, is called Hypogenous and is the one that forms the biggest square. a and b are the two smaller sides.
Proof of Pythagoras Theorem
The Pythagoras Theorem
Prove the Pythagoras theorem
Pythagoras theorem states that: In a Right Angled Triangle, the sum of squares of smaller sides is exactly equal to the square of Hypotenuse side (large side). i.e. a2 + b2 = c2
Take a look on how to show that a2 + b2 = c2
See the figure below:

The area of a whole square (big square)
A big square is the one with sides a + b each. Its area will be:
(a + b) ×(a + b)
Area of the other pieces
First, area of a smaller square (tilted) = c2
Second, area of the equal triangles each with bases a and height b:

But there are 4 triangles and they are equal, so total area =

Both areas must be equal, the area of a big square must be equal to the area of a tilted square plus the area of 4 triangles
That is:
(a + b)(a + b) = c2 + 2ab
Expand (a +b)(a + b): a2 +2ab + b2 = c2 + 2ab
Subtract 2ab from both sides: a2 + b2 = c2 Hence the result!
Note: We can use Pythagoras theorem to solve any problem that can be converted into right Angled Triangle.
Pythagoras Theorem and Trigonometry Revision Questions Form Two Basic Mathematics

B. Trigonometric Rations
Trigonometry is all about Triangles. In this chapter we are going to deal with Right Angled Triangle. Consider the Right Angled triangle below:

The sides are given names according to their properties relating to the Angle .
Adjacent side is adjacent (next to) to the Angle
Opposite side is opposite the Angle
Hypotenuse side is the longest side
Sine, Cosine and Tangent of an Angle using a Right Angled Triangle
Define sine, cosine and tangent of an angle using a right angled triangle
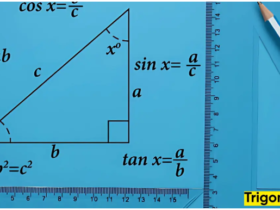
Trigonometry is good at finding the missing side or Angle of a right angled triangle. The special functions, sine, cosine and tangent help us. They are simply one of a triangle divide by another. See similar triangles below:

The ratios of the corresponding sides are:

Where by t, c and s are constant ratios called tangent (t), cosine (c) and sine (s) of Angle respectively.
The right-angled triangle can be used to define trigonometrical ratios as follows:

The short form of Tangent is tan, that of sine is sin and that of Cosine is cos.
The simple way to remember the definition of sine, cosine and tangent is the word SOHCAHTOA. This means sine is Opposite (O) over Hypotenuse (H); cosine is Adjacent (A) over Hypotenuse (H); and tangent is Opposite (O) over Adjacent (A). Or

Example 1
Given a triangle below, find sine, cosine and Tangent of an angle indicated.

Solution



































Leave a Reply