Pressure – Physics Form One Notes
Pressure has many influences on daily life. Knife edges are made sharp to allow easy cutting while football shoes consist of spikes that help the player to have a better grip on the ground. School bags are made with wide shoulder pads to reduce pain on the shoulder and a person carrying a clay pot uses head rings to reduce pain on the head.
All these facts can be explained using the concept of pressure. In this lesson, you will learn about the concept of pressure in solid, liquid, and gas and its applications in daily life situations. The competencies developed will enable you to effectively utilise different tools that operate under the principle of pressure.
Concept of pressure
Consider an iron nail being driven into a piece of a block of wood through its sharp end as in Figure (a) and the flat end as in Figure (b). The iron nail with the sharp point will penetrate easily into the block of wood. On the contrary, when it is driven into the same block through its flat end with the same magnitude of force, it will not penetrate easily.

Driving an iron nail into a block of wood
On the other hand, if two wooden blocks of different surface areas are driven into a soft surface using force of the same magnitude, the block with a smaller surface area will penetrate deeper into the soft surface than the one with a larger surface area, as illustrated in Figure BELOW.

Driving a wooden block into the soft surface
These situations show that when a force acts on an object, the result can be strongly affected by the surface area over which it acts. The relationship between force and the surface area over which it acts can be described by the concept of pressure. When a force is applied in a direction perpendicular to the surface of the object, the object experiences pressure.
Thus, pressure is defined as the force acting normally or perpendicularly on a unit surface area of an object. That is,
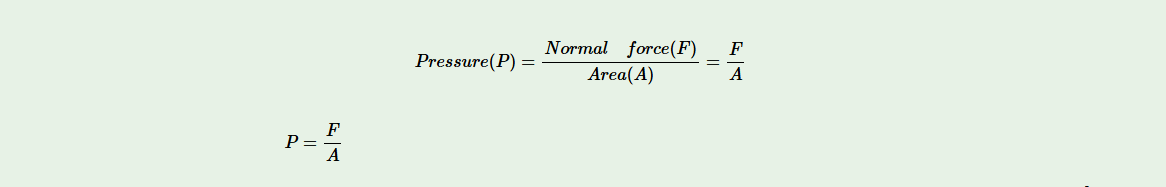
For a given amount of force, the smaller the area of application the larger the pressure exerted. The SI unit of pressure is newton per square metre, (N/m2). This unit is usually referred to as the pascal, Pa, where 1 Pa = 1 N/m2.
Other units of pressure are atmosphere, torr, bar and mmHg.
1 atmosphere (atm) = 760 mmHg.
1 atm = 1 × 105 N/m2 = 1 bar
1 torr = 1 mmHg = 133.3 Pa.
Activity 1
Aim: To demonstrate the concept of pressure.
Materials: Two buckets, one having a thin handle (A) and the other having a thick handle (B) and water
Procedure
1. Fill each bucket with an equal volume of water.
2. Use one hand to lift the buckets containing water, one at a time.
3. Record your observations.
Question
Which of the buckets gave you more pain when lifting? Why?
If you lift a bucket of water with a thin handle, you will experience some pain. However, if the handle is made thicker, the pain will be much less. This is because, for a thicker handle, the area over which the force is applied is large and so, the pressure exerted is small.
Task 1
Discuss the variation of pressure with area in various contexts.
Pressure due to solids
Pressure in solids depends on the surface of contact. A force (F) applied onto a small surface area exerts a greater pressure as compared to when it is applied onto a large surface area.
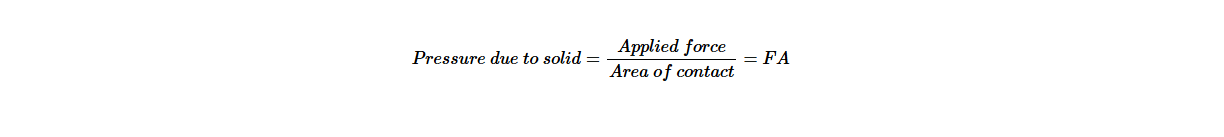
Example 1
A block of wood weighs 3 N and measures 5 cm × 10 cm × 4 cm . If it is placed on a table with its largest base area or smallest area face in contact with the table, it would exert different pressure on the table. Which surface would exert the largest pressure on the table?
Solution



Example 2
The tip of a needle has a cross-sectional area of 1 × 10–6 m2. If a doctor applies a force of 20 N to a syringe that is connected to the needle, what is the pressure exerted at the tip of the needle?


Dependence of pressure on surface of contact
From examples 7.1 and 7.2, it is noticed that the greater the surface of contact, the lower the pressure exerted. Also, the smaller the surface of contact of an object, the greater the pressure it exerts. Generally, to create a large amount of pressure, you can either exert a large force or exert a force over a small area or do both.
Activity 2
Aim: To demonstrate the dependence of pressure on the surface of contact.
Materials: Wires of varying diameters, and bars of soap
Procedure
1. Use a thin piece of wire to cut a bar of soap into half.
2. Use a thick piece of wire to cut a similar bar of soap into two pieces.
3. Record your observations.
Questions
(a) What is the difference between cutting a bar of soap using a thin wire and when using a thick wire?
(b) Explain your observation.

It is easier to cut a bar of soap using a thin piece of wire than a thick one. This shows that the smaller the surface in contact with another, the greater the pressure it exerts. Thus, the pressure between two solid surfaces depends on the force between the surface and the area of contact of the two surfaces.
Applications of pressure due to solids
Pressure due to solids has wide practical applications. The effect of pressure is applicable when using nails, screws, pins, spears and arrowheads. These items are given sharp points to increase their penetration abilities. Figure 7.4 shows examples of solid objects with sharp points.



Objects with sharp points
Knives blades and razor blades have sharp cutting edges, as shown in Figure 7.5. Sharp edges have a minimal area over which an applied force exerts pressure, which facilitates cutting.


Objects with sharp edges
Some living organisms make use of pressure for self-defence. For example, a fish uses its sharp fins to protect itself. The fins inflict pain on an intruder’s body. The fish fins are shown in Figure BELOW.

Fish fins
A sharp heel has a small area over which the body’s weight (force) exerts pressure. Also, it is notable that when one walks on shoes with sharp-pointed heels, shown in Figure 7.7 (a), the sharp-pointed heels exert greater pressure on the ground than the flattened sole, shown in Figure (b).


Sharp-pointed heel and flat sole shoes
During the construction of a railway line, wide wooden or concrete sleepers are placed below the railway tracks, as shown in Figure 7.8. This provides a large surface area over which the weight of the train acts. This is a safety measure for rail tracks.

Railway
Buildings are constructed with wide foundations as seen in Figure 7.9 to ensure that the weight of a building acts over a large area. As a result, the pressure exerted by the building on the ground is considerably reduced.

Foundation of a building
It is painful to walk with bare feet on a road that is covered by pebbles. The weight of the body exerts considerable pressure on the sharp-edged pebbles whose surface area is small. The pebbles exert an equal reaction on the feet.
Exercise 1
Answer all questions
(Use g = 10 N/kg)
1. A rectangular plastic block weighing 1.5 kg rests on a horizontal floor. If it measures 40 cm × 30 cm × 20 cm, calculate the greatest and least pressure that the block can exert on the floor.
2. Calculate the pressure under the feet of a student, given the foot area is 8 cm2 and the student’s mass is 43.8 kg.
3. The mass of a cuboid is 60 kg. If it measures 50 cm × 30 cm × 20 cm, what is the maximum pressure that it can exert on the floor?
4. The density of a Pine wood block is 700 kg/m 3 . If it measures 1⋅5 m × 1⋅ 2 m × 1⋅0 m, calculate the maximum and the minimum pressure exerted by the block.
Pressure in liquids
A liquid will exert pressure on an immersed object as well as on the wall of its container. Note that, the pressure exerted by the liquid at any point in the liquid is due to the weight of the liquid column above the point.
As the depth of the liquid increases, the weight of the liquid also increases and hence the pressure increases. This concept can be explained using the marble pile model. It is important to note that, since the particles in liquid are loosely packed, the pressure acts in all directions. Assume that the molecules of liquid are packed together but are not firmly tight to their neighbours, as shown in Figure below.

Marble pile model
If a downward force is applied shown in Figure 7.10, the marbles are pushed sideways as well as downwards. Similarly, the gravitational force pulls the liquid. This causes the liquid to be pushed out sideways as well, and so the liquid exerts a sideways pressure too.
Calculating the pressure in a liquid
Figure below shows a tank with base area A (m2) filled with a liquid to a height h (m) and the gravity, g (N/kg) pushes liquid molecules down producing the force of gravity or weight (N) in the liquid.
Because the area of the tank is fixed, increasing the height of the liquid in the tank will also increase the weight of the liquid and the pressure, as previously stated. Therefore, the pressure in the liquid depends on the weight of the liquid and the base area of a tank.

Pressure exerted by water in a tank
To calculate the pressure in liquids, consider the liquid column of cross-sectional area, A (m2) at a depth, h (m) below the surface of the liquid. If the density of the liquid is ρ (kg/m3), then,
Volume of the vertical column of liquid = Base area (A) × Height (h) = Ah
The mass due to the liquid column = Volume of liquid × Density of liquid.
= Ahρ
But Force, F = mg = Ahρg

Pressure in liquids = height of the liquid column × density of liquid × acceleration due to gravity.
Thus, pressure at any point in a liquid at rest depends on a depth of the liquid and the density of the liquid. It is important to note that pressure in liquid does not depend on the area of the container.
Characteristics of pressure in liquids
Pressure in liquids is characterised by the following parameters.
1. Pressure in a liquid increases with depth.
2. Pressure in a liquid acts equally in all directions.
3. Pressure in a liquid increases with an increase in the density of the liquid. Mercury exerts more pressure than an equal volume of water because mercury is denser than water.
Variation of liquid pressure with depth
The pressure in a liquid increases with depth of the liquid.
Activity 3
Aim: To demonstrate the variation of pressure with depth of a liquid.
Materials: Water, large can or big plastic bottles, nail, hammer, ruler and cellotape
Procedure
1. Take a large can and punch two holes on opposite sides using a nail and hammer but at the same height from the bottom of the can.
2. Seal the holes using a cellotape.
3. Pour water into the can to a certain height. Simultaneously, unseal both holes and record the horizontal distance covered by the water stream from each hole.
4. Stop pouring water.
5. Punch holes at different heights on a second bottle can but on the same side.
6. Seal the holes as in step 2.
7. Pour water into the can to a height above both holes.
8. Simultaneously, unseal the holes while keeping the water height constant by continuously pouring water into the can.
9. Observe and record the horizontal distance covered by water streams from each hole.
Questions
(a) What causes the water to spurt out of the holes?
(b) From this activity, what can you conclude about pressure in liquids?

The pressure at a certain point in the liquid is proportional to the height of the liquid column above that point. The larger the height above a point, the larger the pressure at that point. Thus, the holes on the can that are at the same level (depth) experience the same pressure and the liquid will be spurted to the same distance. This is because the pressure in liquid acts in all directions. It is also equal at the same depth, as shown in Figure

Water spurting from holes at the same level
The holes punched at different levels on the can will spurt water to different distances. The hole at the top has the least height of liquid above it. This means that the water spurts the shortest distance. This distance increases with an increase in the height above the hole, as shown in Figure

Water spurting from holes at different heights
Therefore, the hole at the bottom of the can will spurt water to the furthest distance. Note that, liquid pressure increases with depth. This explains why the wall of a dam is made much thicker at the bottom than at the top, as shown in Figure

Dam
Consider a liquid that has been released into a communicating vessel shown in Figure 7.15. When water or any other type of liquid is poured into a communicating vessel, it will attain the same level in all of its tubes regardless of shape of the tubes.

Pressure in a communicating vessel
The fact that the liquid rises to the same vertical height in all tubes is an indication that pressure at all points of similar depth in a liquid is the same. A liquid always finds its level in a vessel in which it is contained. Pressure at A, B, C and D in Figure 7.15 is the same.
Task 2
Fill a polythene bag with water and hold or press the upper part. Using a pin, prick the polythene bag randomly. Discuss your observation.
Pressure in liquid and upthrust
When an object is submerged in a liquid, its bottom side experiences a greater pressure than the top side. The difference in pressure between these sides results in an upward force known as upthrust. Figure 7.16 shows an object submerged in liquid.

Variation in pressure producing upthrust
The pressure on the right side of the object increases with increasing depth but is exactly balanced by pressure on the left side so that the net force in the horizontal direction is zero.
Example 3
A cube of sides 2 cm is completely submerged in liquid so that the bottom of the cube is at a depth of 10 cm. If the density of the liquid (ρ) is 1 027 kg/m3, and g = 10 N/kg:
(a) What is the difference between the pressure at the bottom of the cube and the pressure at its top?
(b) Determine the difference in the forces at the top and bottom.
(c) What is the weight of the water displaced by the cube?



Difference in force = 205.4 N/m2 × 0.0004 m2 = 0.0822 N
This is the upthrust acting on the cube.
(c) The weight of water displaced = mass of water displaced ×acceleration due to gravity.
The weight of water displaced = density × volume of water displaced × acceleration due to gravity
But the volume of water displaced = volume of the cube
The length of the cube = width = height of the cube.
Then, Volume of the cube = L3
L3 = (2 cm)3 = 8 cm3 = 0.000008 m3
The volume of water displaced is equal to the volume of a cube = 0.000008 m3
Mass of water displaced
(Mwater) = Density of water × Volume of water displaced = ρVwater
Then,
weight of water = Mass of water × acceleration due to gravity = Mwater × g
Weight of water = 1027 kg/m3 × 0.000008 m3 × 10 N/kg = 0.0822 N
Therefore, weight of displaced water is 0.0822 N.
Example 4
Calculate the pressure exerted on a diver at a depth of 20 m below the surface of water in a sea. Atmospheric pressure = 1.03 × 105 Pa, density of water = 1 000 kg/m3, g = 10 m/s2 or 10 N/kg.

Solution
Pressure due to the water in the sea
= hρg
= 20 m × 1 000 kg/m3 × 10 N/kg
= 200 000 N/m2 = 2 × 105 Pa
Pressure exerted on the diver = Atmospheric pressure + pressure due to the water.
= 1.03 × 105 Pa + 2.00 × 105 Pa
= 3.03 × 105 Pa
Transmission of pressure in fluids
Consider pressure applied to any part of an enclosed vessel containing a fluid. The molecules of fluid are free to move; thus, transmit the pressure equally throughout the enclosed container. This phenomenon was observed by a French scientist and philosopher known as Blaise Pascal in 1650 and it is called the principle of transmission of pressure in fluid.
Pascal’s principle of pressure transmission in fluids states that “When pressure is applied at any point on the surface of a fluid contained in a closed container, it is transmitted undiminished to all parts of the fluid and the walls of the container”.
The principle of transmission of pressure in fluid can be demonstrated using the apparatus shown in Figure 7.17. The apparatus consists of a glass tube fitted with a movable piston and a bulb pierced with uniform-sized holes. Water is filled in by dipping the bulb in water and slowly pulling the plunger.
When pushing the piston in, the water squirts out from all the holes with equal strength. This shows that the piston exerts force per unit area (pressure) on the water which is then transmitted equally throughout the water. Pascal’s principle is widely used in many devices. Hydraulic car jacks, car brakes, and most of the mechanical diggers and bulldozers use the principle of transmission of pressure in fluid in their operations, and hence the name hydraulic machine.

Illustration of the Pascal’s principle
The hydraulic press
The hydraulic press uses Pascal’s principle to convert a small force into a large force and vice versa. Consider a liquid confined in a container that is fitted with two pistons of different diameters, hence different cross-sectional areas. Figure 7.18 shows a simplified form of a hydraulic press.
A downward force applied to piston 1, produces pressure P1 which is equally transmitted throughout the liquid into piston 2. Since piston 1 has a smaller area than piston 2, a small force applied on piston 1 is multiplied at piston 2. Thus, a smaller force in piston 1 creates a larger force in piston 2.

Hydraulic press

Since A2 is larger than A1, F2 is also larger than F1 so the output force is larger than the input force. A small force, F1 applied at piston 1 can produce a larger force, F2 to lift a very large weight resting on piston 2. A hydraulic press is a force-multiplying device. Its multiplying factor is A2/A1.
As the small piston is pushed down, the large piston is pushed up. However, the two pistons do not move through the same distance, d. The smaller piston moves through a larger distance than the large piston.
The distance, d moved by the piston is inversely proportional to the cross-sectional area:
d1/d2=A2/A1
Therefore, d2 = D1A1/A2
Example 5
The pistons of a hydraulic press have their areas given as 0.0003 m2 and 0.02 m2 , respectively. If the small piston is pushed down with a force of 120 N, what is the force on the large piston?


Example 6
A hydraulic press has pistons with areas of 0.02 m2 and 0.1 m2 as shown in Figure 7.19. A car weighing 5 000 N sits on a platform mounted on the larger piston.
(a) How much force must be applied to piston 1 to lift the car?
(b) How far must piston 1 be pushed downward to raise the car 0.3 m?


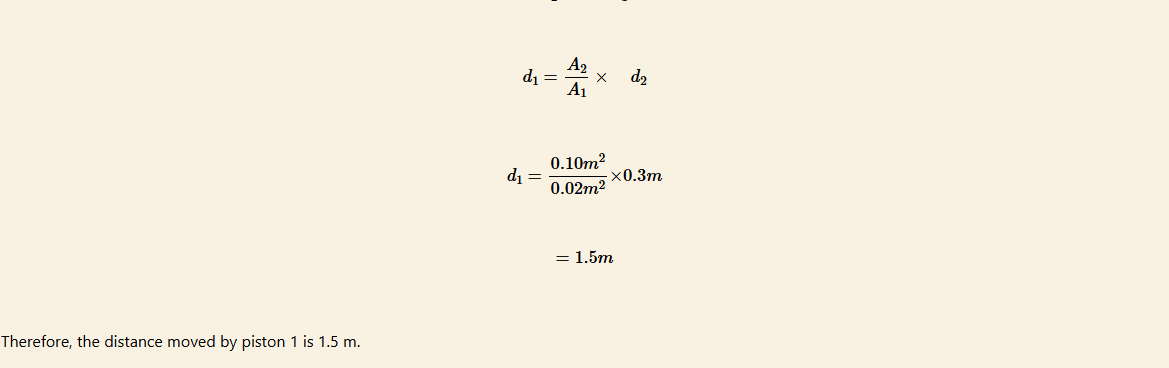
Applications of the hydraulic press
1. A hydraulic press can be used in industries to compress bulky items. The purpose is to compress a large object such as a bale of cotton into a small size for more economical transport, as shown in Figure

Compressing bale of cotton
As the small piston is pushed down, the large piston is pushed upwards compressing the bale of cotton. The amount by which the force applied to piston 1 is increased depends on the ratio of the areas of the two pistons.
2. Another application of the hydraulic press is in hydraulic brakes, as shown in Figure

Hydraulic brake system
When pressure is applied to the brake pedal, it pushes the piston in the master cylinder forward creating pressure in the brake fluid. This pressure is transferred to the slave cylinders where the force is multiplied and pushes the brake shoes against the brake drum that is attached to the wheel of the vehicle.
Friction between the brake shoes and the drum slows down the wheels’ rotation. There are identical systems on all four wheels ensuring the same braking force on each wheel so that the vehicle slows down uniformly. When the pressure on the brake pedal is removed, the return spring pulls the brake shoes away from the drum and the wheels become free to rotate.
3. It is used in industries in the forming of metals.
4. Since the hydraulic press acts like a lift, it is used for lifting heavy loads. The pressure applied on the small piston creates a large force on the large piston which lifts the load. Figure 7.22 shows a crane lifting a heavy load.

A crane lifting a heavy load
Measuring pressure using a manometre
A manometre is a simple device used to measure pressure (commonly gas pressure). It uses the property that the pressure due to the weight of a fluid of constant density is given by
P = hρg.
The simplest form of a manometre consists of a U-shaped tube filled with a liquid of a known density. The liquid is normally coloured to enhance visibility. The manometre is filled with the liquid until both sides of the tube are half-fi lled, as shown in Figure


Manometer
When both ends of the tube are open, the pressure on both sides is equal. This water level is marked as zero point as in Figure 7.23 (a). When one end of the tube is connected to the unknown pressure P1 , the liquid level falls in one arm and rises in the other arm as shown in Figure 7.23 (b). The change in height (Δh) is caused by the change in pressure (ΔP) which can be obtained from the equation,
P1 = P2 + (Δh)ρg.
Since, a manometre measures pressure by comparing it with atmospheric pressure, it is sometimes called a gauge pressure.
Task 3
Demonstrate the use of a manometre in measuring the pressure of a liquid. Measure the pressure of different liquids using the manometer.
Atmospheric Pressure
The surface of the earth is surrounded by the atmosphere, which is the layer of air consisting of a mixture of gases. Atmospheric pressure is a result of the weight of this layer of gases. This is why air pressure is usually referred to as atmospheric pressure. The atmospheric pressure on the earth’s surface and objects on the earth is approximately 1.01 x 105 N/m2 or 1 atmosphere. We do not experience this great pressure because the fluids in our bodies exert pressure slightly greater than the atmospheric pressure.
Variation of atmospheric pressure with altitude
The pressure exerted by the atmosphere decreases with an increase in altitude from the mean sea level. For example, atmospheric pressure is found to be higher at the base and lower at the top of Mount Kilimanjaro as shown in Figure 7.24. This variation is due to the fact that the density of air is high at the mean sea level and decreases with altitude (air exerts less pressure) above the mean sea level.
The variation of pressure with altitude has a practical impact on human life. Mountain climbers may face nose bleeding at high altitudes above the mean sea level because of the higher blood pressure compared to atmospheric pressure. It is important to note that astronauts wear space suits to maintain this pressure.

Variation of atmospheric pressure with altitude along Mount Kilimanjaro
The values of atmospheric pressure at some regions above and below sea level are shown in Table

It can be generalized that atmospheric pressure at any given point of constant g depends on two factors:
(i) density (ρ) of air; and
(ii) height (h) of air column.
Thus, atmospheric pressure P, can also be expressed as, P = hρg.
Change of pressure during flight and landing of airplane
Passengers on aeroplanes frequently swallow saliva during flight and landing due to various factors related to changes in cabin pressure and the natural responses of the body. Swallowing helps equalize the pressure in the ears and sinuses, preventing discomfort or pain caused by rapid pressure changes during take-off and landing.
Additionally, the body continuously produces saliva, and swallowing clears excess saliva from the mouth and throat. Dry cabin air can increase saliva production, and swallowing also helps alleviate the sensation of thirst and moisten the throat. Nervousness, habit, and subconscious response to any throat discomfort also contribute to this natural behaviour.
While generally not a cause for concern,passengers experiencing severe discomfort should seek assistance from flight attendants or healthcare professionals.
Example 7
A commercial aeroplane is cruising at an altitude above sea level. At take off the plane was at a pressure of 1 atm. What additional pressure should the cabin be pressurized to normalize the pressure to 1 atm at this height if a pressure measuring instrument indicates a height difference of 600 mmHg?


Example 8
A mercury barometre in a physics laboratory reads 732 mmHg. Calculate the atmospheric pressure in Pascal.
(Given density of mercury, ρ = 1.36 × 104 kg/m3 and acceleration due to gravitational g = 9.8 N/kg)


Exercise 2
1. (a) Can high altitude cause difficulty in breathing? Why?
(b) At a given place, a mercury barometre records a pressure of 0.50 m of Hg. If mercury in the barometre is replaced by water. What would be the height of the water column? Take R.D. of mercury = 13.6.
2. Explain why:
(a) There is a possibility of nose bleeding at high altitude.
(b) Our ears pop when going on mountain. What is going on in our body and why does yawning help to solve the issue?
3. Does atmospheric pressure add to the gas pressure in a rigid tank of gas? In a toy balloon? When, in general, does atmospheric pressure not affect the total pressure in a fluid?
Evidence for the existence of atmospheric pressure
The existence of atmospheric pressure can be verified experimentally using the following apparatus:
1. Magdeburg hemispheres.
2. Water covered with cardboard.
3. Crushing can.
Magdeburg hemisphere
Magdeburg hemispheres are two half-spheres of equal size joined to form an air tight sphere. Placing them together traps air between them. This air is merely trapped and not compressed, thus the pressure inside is the same as the pressure of the atmosphere outside the spheres as shown by arrows in Figure 7.25 (a). In this case, one can pull the spheres apart with nearly no resistance.

Action of Magdeburg hemisphere
Now, what happens if all the trapped air inside the hemispheres is removed? On removal of air from inside, a partial vacuum is created inside the sphere. Thus, the external atmospheric pressure exerts a large unbalanced force and presses the spheres tightly together. Therefore, it becomes very difficult to pull the half-spheres apart.
Activity 4
Aim: To demonstrate the existence of atmospheric pressure using water in a tumbler.
Materials: Glass tumbler or test tube, cardboard, water and plunger
Procedure
1. Fill a glass tumbler with water and place the cardboard firmly on top of the glass so that there is no air between the glass and the cardboard.
2. With your hand on the cardboard, gently turn the tumbler upside down, as shown in Figure 7.26, then, remove your hand from the cardboard.
3. Record your observations.

Questions
(a) Explain why the cardboard does not fall when the glass tumbler is inverted.
(b) Explain your observations.

The cardboard does not fall when the glass tumbler is inverted due to the atmospheric pressure acting upwards on the cardboard. Atmospheric pressure is higher than that of the water acting downwards on the cardboard.
Activity 5
Aim: To demonstrate the existence of atmospheric pressure using a crushing can.
Materials: Empty tin, hot water, cold water and cork
Procedure
1. Pour a small quantity of hot water into a can and boil for a few minutes while the can is open to drive off the air, as shown in Figure 7.27 (a).
2. Stop boiling and then close the can tightly with the cork.
3. Pour some cold water over the can to cool it as in Figure (b).


Questions
(a) What happens to the can?
(b) Explain your observation.

Steam emerging from boiling water drives out air from the can. When the can is cooled by cold water the steam condenses, leaving a partial vacuum inside the can. Consequently, the higher atmospheric pressure outside the can crush it inwards.
Measurement of atmospheric pressure
Atmospheric pressure is commonly measured by using a barometer. In this section, you will learn three types of barometers, namely simple barometer, Fortin barometre and aneroid barometer.
Simple barometre
A simple barometre is the most fundamental of the other types of barometers. The barometric liquid used is mercury. A simple barometre consists of a hard glass tube closed at one end and a glass trough filled with mercury as shown in Figure

A simple barometer
Atmospheric pressure pushes mercury to a height of 76 cm at mean sea level.
Activity 6
Aim: Constructing a simple mercury barometer.
Materials: Thick-walled glass tube about 1 m long sealed at one end, mercury and glass trough

Procedures
1. Fill the glass tube with mercury to almost the top of the tube.
2. Ensure that no air bubbles are trapped on the wall of the glass tube. This is done by closing the open end with a finger and inverting it several times.
3. Now, fill the tube completely with mercury.
4. With a finger closing the open end, invert the tube into the trough of mercury. When the finger covering the open end is removed, the mercury is seen to settle to a height of about 760 mmHg.
Note: Mercury should be handled with care to avoid poisoning.
Questions
(a) Why is it necessary to close the open end of the tube when making a simple mercury barometer?
(b) What happens when a bubble of mercury is trapped in the simple barometer?
(c) Why can’t water be used as a barometric fluid?

Fortin barometre
A Fortin barometre is a modified simple barometer. It consists of an inverted tube closed at its upper end with the lower open end immersed in a reservoir of mercury, as shown in Figure 7.30. There is a vacuum at the upper end.
As the atmosphere pushes down on the mercury in the reservoir, the pressure is transmitted throughout the mercury, specifically to the open end of the tube. This pressure forces some of the mercury up into the tube until the height of the column of mercury exactly balances the atmospheric pressure. The atmospheric pressure is measured in terms of the height of the column of mercury.

Fortin barometer
Before taking the readings, the mercury level is adjusted by the screw until it touches the ivory point.
However, the use of the mercury in a Fortin barometre has the following disadvantages:
1. Mercury is very expensive and toxic to use.
2. Mercury is in the form of liquid and the column is approximately 1 m tall, so it is not portable.
3. The Fortin barometre must be mounted in a vertical position.
Aneroid barometre
An aneroid barometer, shown in Figure 7.31, is a type of barometre for measuring atmospheric pressure without the use of a liquid, hence the word ‘aneroid’ means without fluid. It consists of a partially evacuated metal chamber and a thin corrugated lid which is displaced by variations in external pressure.
A lever connected to the diaphragm of the chamber moves a pointer. Any change in pressure would cause the box to be squashed or expanded. The small deformation of the box will trigger a larger motion in the scale pointer using the lever.

Aneroid barometer
The aneroid cell is prevented from collapsing under the pressure of the atmosphere by a strong spring. The spring is attached through a set of levers to a pointer that indicates the pressure on a calibrated scale, as shown in Figure 7.31 (b). Even though it contains no mercury, the pressure is still measured in units of mmHg.
Task 4
Discuss why it is advantageous to use the aneroid barometre instead of the Fortin barometer.
Common devices utilizing atmospheric pressure
There are a variety of common and even simple devices that make use of atmospheric pressure. These include drinking straws, cupping therapies, siphons, bicycle pumps, lift pumps, force pumps, vacuum cleaners and syringes.
Siphon
A siphon is a continuous tube that allows liquid to drain from a reservoir through an intermediate point that is higher than the reservoir. The liquid can flow without pumping because of pressure difference. To do this the end of the long arm has to be lower than the surface of the liquid in the reservoir as shown in Figure

The siphon principle
The liquid rises in the tube because it is pushed by atmospheric pressure. The atmospheric pressure acts on both ends of the siphon but the long arm carries more weight of the liquid. Then, the force of gravity draws the liquid through the long arm and this maintains the low pressure that is established at the start. Once started, the siphon does not require additional energy to maintain liquid flow out of the reservoir. The siphon will pull the liquid out until the level in the reservoir falls below the intake point.
Activity 7
Aim: To demonstrate the principle of the siphon.
Materials: Rubber tube, water and two empty cans
Procedure
1. Pour water into can 1 up to about halfway and set it on the edge of a table.
2. Set an empty can 2 on the floor underneath can 1 on the table.
3. Take a piece of rubber tubing that is long enough to reach both cans and fill it with water.
4. Cover both ends of the tube with your fingers (you may need a partner to do this).
5. Immerse one end of the tube into the can with water and the other end into the empty can.
6. Uncover both ends of the tube and observe what happens.
Question
Does the water flow from one can to the other? Explain.

Applications of siphon
Siphon is applied in many areas and devices that are used every day.
1. It is used in the toilet flushing systems (chain and ball tank). The flush is triggered by a handle that operates a simple diaphragm like piston pump that lifts enough water. The same procedure is used in the automatic flushing tank, which does not require a handle to trigger the flushing.
2. It is used to drain excess water in special rain gauges called siphon rain gauges.
3. A siphon cup is a reservoir attached to a spray gun.
4. It is used to drain water in some drainage systems.
Task 5
Discuss the application of siphon in the automatic flushing tank and toilet flushing system. Discuss other areas where the siphon is applied.
Vacuum cleaner
A vacuum cleaner shown in Figure 7.33 is used in cleaning floors and carpets. It also utilizes the atmospheric pressure to work. When it is on, the fan inside the cylinder blows air out as a result, a partial vacuum is created inside. This makes the atmospheric pressure outside the cylinder higher; hence forcing air and dust particles into the cleaner.

The vacuum cleaner
Plunger
A plunger shown in Figure 7.34, is a cup-like rubber sucker, with a long handle at one end. When used correctly, a plunger can unclog pipes and make them operate smoothly. Sometimes pulling the plunger is not easy. For example, if it is pressed hard on a table surface, all the air between it and the table can be squeezed out, hence creating a vacuum. In that case, the plunger will stick to the table because of the higher atmospheric pressure outside.

Plunger
Lift pump
A lift pump is used to raise water from underground sources. This is a pump that is used to lift the liquid, rather than force liquid up. This pump is illustrated in Figure

Lift pump
The handle operates a reciprocating mechanism that raises and lowers a piston with a transfer valve at its centre. The piston acts to separate the pump cylinder into upper and lower chambers and the transfer valve controls the flow of water between them. At the bottom of the lower chamber is an intake valve that controls the flow of water from the external source. The pump starts with the piston at the bottom of the empty cylinder and both valves closed.
The pump handle is then pushed down lifting the piston upwards. The transfer valve remains closed and the intake valve opens to allow water from the external source to fill the lower chamber. This is due to the low-pressure region created between the transfer valve and the piston.
The handle is lifted upwards pushing the piston down. The intake valve closes and the transfer valve opens allowing water to pass into the upper chamber.
The pump handle is pushed down again lifting the piston upward. The transfer valve closes and the intake valve opens to allow water from the external source to fill the lower chamber. The water in the upper chamber is lifted and flows out of the spout.
The process is repeated; hence, it is continuous. Atmospheric pressure can support a water column of about 10 m. This means that the pump cannot be higher than 10 m above the water level.
Task 6
Using online and other sources discuss the main features, mode of operation and limitations of a lift pump. What are the uses of a lift pump in your daily life?
Force pump
A force pump is a modification of a lift pump. It consists of a cylinder fitted with a solid piston, as shown in Figure 7.36. There are intake (B) and output valves (A). The piston is moved up and down by a motor or by hand.
When the piston moves up, the intake valve opens and the output valve closes due to the low pressure created between the piston and the intake valve. This draws water from the external source into the pump cylinder. When the piston moves down, the intake valve closes and the output valve opens; this forces the water in the cylinder to go out of the pump.

Force pump
A force pump moves water from deeper depths than the lift pump.
Syringe
A syringe is a simple pump that consists of a plunger that fits in a cylindrical tube, as shown in Figure 7.37. The plunger can be pulled and pushed inside the tube or barrel. When the plunger is pulled out, the pressure inside the cylinder decreases; this makes the atmospheric pressure higher than the pressure inside the cylinder.
Thus, the surrounding fluid is pushed into the syringe. When the plunger is pushed, the fluid in the syringe is expelled since the pressure in the syringe becomes higher than the atmospheric pressure. This enables the syringe to take in and expel fluid through the opening (nozzle) at the end of the tube.

Syringe
Task 7
Carefully observe the syringe and use it to take in and expel different fluids. Investigate and list down situations in our everyday life where the syringe is used.
Uses of the syringe
The following are the uses of a syringe:
1. A syringe can be fitted with hypodermic needles and used to administer injections. The injectable medicine is expelled through the needle into the body of a patient by pushing the plunger.
2. A syringe is used to measure or draw liquids in a laboratory.
3. A syringe is used to apply certain compounds such as glue or lubricant.
Bicycle pump
A bicycle pump is a type of force pump that consists of a hollow metal cylinder and a movable piston. It is specifically designed for inflating bicycle tyres. The piston consists of a cup shaped leather washer which is fixed to a metal rod by a metal washer, as in Figure 7.38 (a).
When the piston is pulled out, a low pressure is created in the region just below the leather washer. Atmospheric pressure then forces air into the pump through the inlet valve as in Figure 7.38 (b).
When the piston is pushed forward, the trapped air below the piston is compressed and the tube of the bicycle can be inflated using a valve as shown in Figure (c).

Operation of a bicycle pump
Task 8
Visit a nearby bicycle repair shop and observe a bicycle pump. Discuss its mode of operation. Draw a well-labelled diagram of the bicycle pump. What is the significance of the intake and outlet valves?
Chapter summary
1. Pressure is defined as the force acting normally per unit surface area.
Pressure=Force/Area
2. The SI unit of pressure is N/m2 . Other units of pressure are Pascal (Pa), atmosphere (atm), torr and mmHg.
3. Fluids (liquid or gas) exert pressure on an immersed object and the walls of their container. The pressure in the fluid at a depth h is given by P = ρgh. Pressure in a liquid depends on the density of the liquid and the depth.
4. Pascal’s principle states that, any pressure applied on the surface of an enclosed fluid will be transmitted equally to all points in the fluid. This principle is the basis for the hydraulic lift, hydraulic press and hydraulic brakes. Pressure in liquids and gases can be measured with a manometre that works on Pascal’s principle.
5. Air pressure is measured using either a Fortin barometre or an aneroid barometer.
6. Standard atmospheric pressure at sea level is 101.3 kPa.
7. Siphons, syringes, lift and force pumps are used to transfer liquids and gases.
Revision Exercise
Section A
1. Choose the most correct answer.
(i) Which expression has the same units as the SI unit of pressure?

(ii) Some doctors measure blood pressure by using a mercury manometer. Blood pressure varies by 5.6 kPa as a heart beats. The density of mercury is 14 000 kg/m3 and the gravitational field strength g is 10 N/ kg. What is the change in the height difference between the levels in the manometre during a heartbeat?
(a) 40 mm
(b) 80 mm
(c) 400 mm
(d) 800 mm
(iii)Five blocks have the same mass but different base areas. They all rest on a horizontal table as shown in Figure

A graph is plotted to show the relationship between the pressure exerted on the table and the base area of the block. Which graph shows this relationship?


(iv) The diagram in Figure 7.41, shows a rectangular block of mass 8.2 kg immersed in sea water of density 1100 kg/m3. What is the difference in pressure between the top and the bottom surfaces of the block?

(a) 220 Pa. (b) 2 200 Pa . (c) 18 000 Pa. (d) 23 000 Pa
(v) A horizontal plate of area 0⋅036m2 is beneath the surface of coconut oil with a density of approximately 930 kg/m3. The force on the plate due to the pressure of the oil is 290 N. What is the depth of the plate beneath the surface of the oil?
(a) 0.87 m. (b) 1.13 m. (c) 8.7 m. (d) 9.1 m.
(vi) Each tyre of a car has an area of 100 cm2 in contact with the ground. The car has a mass of 1600 kg. The weight of the car is equally distributed amongst the four tyres. The gravitational field strength g is 10 N/kg. What is the pressure exerted on the ground?
(a) 4.0 N/cm2 (b) 16 N/cm2 (c) 40 N/cm2 (d) 160 N/cm2
(vii) The depth of water in a bath varies from 20.0 cm at the shallow to 30.0 cm at the end of the plug, as shown in Figure

What is the pressure of water acting on the plug? The density of water is 1 000 kg/m3.
(a) 0.98 kPa. (b) 2.0 kPa. (c) 3.0 kPa. (d) 1.06 kPa.
(viii) A manometre contains mercury of density 14 000 kg/m3. The manometre is connected to a gas supply and the difference in the height of the mercury levels is 72 mm. The atmospheric pressure is 100 kPa. The gravitational field strength g is 10 N/ kg.

What is the pressure of the gas supply?
(a) 90 kPa (b) 99 kPa (c) 110 kPa (d) 200 kPa
(ix) A barometre is an instrument used to measure atmospheric pressure. In one type of barometer, the height of a liquid in a tube is measured. In which diagram does the height h represent atmospheric pressure?


(x) Match each item from Column A with its corresponding item in Column B. Then, write a letter of the correct response in the provided space.

Section B
2. (a) Describe the concept of pressure.
(b) State the SI unit of pressure.
(c) Name devices that are used for measuring pressure.
3. State Pascal’s principle.
4. (a) How can the pressure of a gas be measured?
(b) The open end of a rubber tubing of a mercury manometre is placed in a fluid of density 1.2 g/cm3. The mercury in the manometre rises by 3.0 cm. What is the depth of the fluid at the end of the rubber tubing? (Density of mercury = 13.6 g/cm3).
5. Explain why hitting an inflated balloon with a hammer will not cause it to burst but sticking it with a pin will.
6. A can holds water with a constant depth of 0.5 m. Hole A is punched in the can 0.1 m below the surface of the water and hole B is punched 0.4 m from the surface. From which hole will the water spurt the furthest? Explain your answer.
7. A curved, glass tube is open at one end and sealed at the other. A dense liquid is poured into the tube. The liquid traps air in the sealed end. Figure 7.44 shows the tube, the liquid and the trapped air.

The difference between the liquid levels is h. At room temperature, h is 0.57m. The density of the liquid is 1.4 × 104 kg/m3 or 14 000 kg/m3. The gravitational field strength g is 10 N/kg and the atmospheric pressure is 1.0 × 10 5 Pa. Calculate the pressure of the trapped air.
8. Why are dam walls constructed thicker at the bottom than at the top?
9. Explain why a diver at the bottom of a dam experiences the greatest pressure
10. A can holds water with a constant depth of 0.5 m. The surface of the water is exposed to the atmosphere. What is the pressure on the bottom of the can? (g = 10 N/kg and atm. pressure = 101.3 kPa).
11. (a) A submarine has a surface area of approximately 82 000 m2. If it is travelling at a depth of 0.3 km in the ocean, what is the total force on the submarine’s outer hull? Use the density of seawater 1 100 kg/m3.
(b) Winds in the atmosphere blow from regions of high atmospheric pressure towards regions of low atmospheric pressure. Would you expect the wind to blow from warm regions to cooler ones or from cooler to warmer areas? Explain your answer.
12. In a hydraulic brake system, the piston in the master cylinder has a diametre of 2.0 cm and the piston in the slave cylinder has a diametre of 3.5 cm. The brake pedal is pushed down 10 cm with a force of 50 N. How far do the brake shoes move and with what force do they press against the brake drum?
13. Explain why it would not be practical to make a Fortin-type barometre with water instead of mercury. Hint: Compare the densities of water and mercury.
14. Both the aneroid barometre and the Fortin barometre are used to measure pressure. The working principles and mechanisms of these two objects differ. How can one distinguish between the two?
15. If a passenger swallows their saliva every 20 seconds during take-off, and the take-off lasts for 2 minutes, how many times will they have swallowed during take-off alone?