Sinking and Floating
Sinking and floating is a fundamental phenomenon with practical applications in a wide range of fields, including ship building, marine engineering, and even understanding the behaviour of gases in the atmosphere.
Archimedes’ principle and the law of floatation are important laws of physics that explain the nature and mechanism of sinking and floating. Understanding these concepts is essential for designing stable and buoyant structures that can navigate fluid environments effectively.
In this lesson, the concept of sinking and floating, Archimedes’ principle and the law of floatation will be discussed. Competencies developed will enable you to efficiently use the phenomenon of floating and sinking in your daily activities.
Concept of sinking and floating
When an object is placed in water, it either sinks (goes down into the water) or floats (stays on the surface of the water). Figure 5.1 (a) shows a sealed empty plastic bottle floats on water because its weight is less than the upthrust exerted on it by water.

Sinking and floating
While the sand-filled bottle shown in Figure 5.1 (b) sinks because its weight is larger than the upthrust acting on the bottle. Therefore, floating is the tendency of an object suspended in water to stay on the surface of the water. On the other hand, sinking is the tendency of an object to go to the lower level of water.
Whether an object floats or sinks in a fluid depends on its relative size, weight, and the upthrust acting on the object. If the weight of the object is greater than the upthrust, the object moves downward and therefore sinks.
If the weight of an object is less than the upthrust, the object will stay on the surface of the fluid and therefore float. The action of weight and the upthrust on an object in the fluid is shown in Figure below

In Chapter Two, it was shown that when an object is immersed in a fluid, it displaces a volume of the fluid equal to the volume of the body. It is also shown in the previous section that the upthrust acting on the immersed object depends on the volume of the object and the density of the liquid in which it is immersed. Therefore, sinking and floating can also be explained in terms of the density of the object and that of the fluid.
If the object’s density is greater than that of the fluid, the object will sink. The object floats if its density is less than that of the fluid. Ships and boats float on water because their average density is less than the density of water.
Inflated balloons float in air because their average densities is less than the density of air. Metallic objects, such as spoons and coins, sink in water because they have higher average densities than the density of water.
Task 1
The density of aluminium foil is 2.7 times that of water. Take a piece of foil, shape it into a ball, and place it in water, will it submerge? Explain the factors that determine whether it sinks or floats, and discuss any possible methods to make it sink.
Activity 1
Aim: To demonstrate sinking and floating of objects.
Materials: Various objects of different shapes and sizes (examples are metal spoon, plastic bottle cap, wooden block, rubber ball, Aluminium foil, toy boat), large container filled with water (a basin or a bucket) and paper pencil.
Procedure
1. Predict which object will sink and which one will float. Record your results.
2. Fill the container with water.
3. Wear sanitary gloves, and gently put an object in the water at a time. Observe if it sinks or floats.
4. Repeat step 3 for every object at your disposal.
Questions
(a) What do you notice about the objects that sank?
(b) What do you notice about the objects that floated?
(c) Were there any surprising results or objects that didn’t behave as you predicted?
(d) In terms of density, compare the objects that sank and those which floated.

Conditions for floating
For an object to float, the upthrust exerted by the surrounding fluid must be greater than the objects weight. Upthrust depends on the volume of the submerged part of the object and the density of the surrounding fluid. Thus, when an object is placed in a fluid, the greater the submerged volume of the object, the greater the upthrust.
A ship is normally built with a large hollow space. Typically, the ship has a large volume which allows it to displace a large volume of water, resulting into a large upthrust equalising the weight of the ship. If the hollow space is filled with air, the average density of the ship material and air is less than the density of water and so, the ship floats.
Therefore, the following conditions must be satisfied for an object to float in water:
(a) The volume of the submerged part of the object must be large enough to displace a large volume of water.
(b) The average density of the object must be less than the density of the fluid in which it floats; and
(c) The upthrust due to water must be greater or equal to the total weight of the object.

Task 2
Some water bodies such as the dead sea are known to have abnormally high concentrations of salt. Discuss why a human body sinks in the normal oceans but floats on the dead sea.
Concept of upthrust
Task 3
Hold a stone in one hand and sense its weight. Tie the same stone using a string and submerge it in water. Hold the string and try to pull it. What do you feel about its weight?
Consider a cork being held at the bottom of a beaker that contains a liquid, as shown in Figure 5.3 (a). When the cork is released, it immediately rises to the surface of the liquid, as shown in Figure (b).

The rising of the cork shows that, while inside the liquid, an upward force acts on it. Since this force is greater than the weight of the cork, it is pushed up to the surface of the liquid. An upward force acting on an object that is totally or partially immersed in a fluid is called an upthrust or buoyant force. Upthrust enables an object to float or feel lighter in a fluid.
When one swims in water, his or her weight is balanced by the upthrust acting on the body. Water vessels, like ships and boats, float and sail on water due to this force, otherwise, they would sink.
The tendency or ability of an object to float on a fluid suspended on it is called buoyancy and the upward force exerted by a fluid on that object is called upthrust (buoyant force).
Buoyancy is the force that determines whether an object will sink, float, or remain suspended in a fluid. This concept was best described by Archimedes, who famously shouted “Eureka!” when he discovered the phenomenon.
In addition, an object is said to experience neutral buoyancy when its average density is equal to the density of the surrounding fluid. In this state, the buoyant force is precisely equal to the gravitational force acting on the object, resulting in a net force of zero.
As a consequence, the object remains suspended at a specific depth in the fluid without any vertical acceleration. Neutral buoyancy is particularly important in various fields, including:
Scuba diving; divers use buoyancy control devices (BCDs) to achieve neutral buoyancy, allowing them to hover at a desired depth without sinking or floating to the surface.

Underwater research and engineering; neutral buoyancy is employed in underwater laboratories and simulators to conduct experiments and train astronauts for spacewalks (extravehicular activities or EVAs) as the microgravity conditions in space are similar to those of neutral buoyancy.

Marine biology; researchers and divers use neutral buoyancy to study marine life without disturbing the natural environment.

Apparent weight of an object
If one attempts to lift an object in a swimming pool and then attempts to lift the same object outside of the pool, it feels much lighter in the pool than when outside. This is the effect of upthrust. When a body is totally or partially immersed in a fluid, it experiences an upthrust exerted by the fluid.
The upthrust is equal to the weight of the fluid displaced by the immersed object. Because of upthrust, an object that is submerged in the fluid appears to weigh less than its actual weight in air.
The weight of the submerged object is known as apparent weight, while its weight in air is referred to as the actual weight. The difference between the weight and the apparent weight of an object is referred to as the apparent loss in weight.
Therefore,
Apparent loss in weight = Actual weight – Apparent weight of body in fluid.
= Weight of the displaced fluid
= Upthrust
Thus, Upthrust = Apparent loss in weight.
Activity 2
Aim: To determine the apparent loss in weight of objects immersed in water.
Materials: Measuring cylinder, spring balance, solid objects such as stones, water, string.
Procedure
1. Tie the stone using a string and measure its weight in air using a spring balance as shown in Figure 5.4. Record this weight as w1.

2. Fill a measuring cylinder with water to about 30 ml of its volume.
3. Lower the stone suspended at the end of the spring balance into the water. It should be partially immersed. Note the reading on the spring balance as w2 and the level of liquid in the measuring cylinder.
4. Lower the stone such that it is totally immersed in the water, as shown in Figure 5.4 and record this weight as w3 .
5. Remove the stone, dry and re-weigh it in air. Record this weight as w4 .
6. Calculate the apparent loss in weight of the stone and record it as wL .
7. Repeat steps 1 to 6 for other objects, one at a time.
Questions
(a) What do you notice about the values w1, w2, w3 , w4, and wL?
(b) What is your conclusion about the weight of the stone?

In Activity 2, you have learnt that, the weight of an object in air (w1) is larger than its weight when it is submerged in water (w2). That is, there is an apparent loss in weight (wL) which is the difference between the weight in air and the weight in liquid. Thus,
Apparent loss in weight = weight in air – weight in water.
wL = w1 – w2 or wL= w1 – w3
Note that the apparent loss in weight is equal to the upthrust exerted on the object by water.
Task 4
Suspend a slotted mass of 50 g by a thread from a spring balance. Note the reading of the spring. Pour 60 cm3 of water into a measuring cylinder and immerse the suspended mass in water. (Ensure that the mass does not touch the walls of the cylinder).
Record the readings on the spring balance and on the measuring cylinder. Repeat the same procedure using 100 g and 200 g masses. Illustrate your work using clear diagrams.
Archimedes’ Principle
If an object is immersed in water, it displaces some of the water. The relationship between the upthrust acting on a body and the weight of the displaced fluid, when the body is partially or totally immersed in the fluid was discovered by a Greek scientist known as Archimedes. This relationship is explained by Archimedes’ principle, which is referred to as the law of buoyancy.
Archimedes’ principle states that, “Any object partially or totally immersed in a fluid experiences an upthrust equal to the weight of the fluid displaced by the object”.
It is important to note that the weight of an object acts downwards while the upthrust exerted by the displaced fluid acts upwards.
Verification of Archimedes’ principle
To verify the Archimedes’ principle, perform the following activity.
Activity 3
Aim: To verify the Archimedes’ Principle.
Materials: Beaker, eureka can, spring balance, measuring cylinder, stone, water and digital balance.
The setup is shown in Figure

Procedure
1. Measure the weight of the stone in the air using a spring balance and record its weight.
2. Using a digital balance, measure the mass of a dry empty measuring cylinder, and record its mass.
3. Pour water into a eureka can up to its spout level.
4. Place the measuring cylinder under the spout of the eureka can.
5. Weigh the stone when it is totally immersed in water and record its weight. Wait until all the displaced water overflows into the measuring cylinder.
6. Weigh the measuring cylinder containing the displaced water. Record its weight.
Questions
(a) Determine the mass of the displaced water.
(b) Calculate the weight of the displaced water.
(c) Calculate the upthrust exerted by water on the stone.
(d) How does the upthrust relate to the weight of the displaced water?
(e) Using the results from this activity and your own words, state the Archimedes’ principle.

In activity 3, you observed that upthrust is equal to the weight of the displaced fluid. This observation verifies Archimedes’ principle, which applies to objects of densities. It is important to note that upthrust depends on the weight of the fluid displaced.
Example 1
In an experiment to study the behaviour of the weight of an object a student finds that the weight of the object is 4.9 N in air and its weight when completely submerged in water is reduced to 3.1 N. Calculate the upthrust.

Solution
Weight of the object in air = 4.9 N
weight of the object in water = 3.1 N
upthrust = weight of an object in air − weight of an object in water
= 4.9 N − 3.1 N
= 1.8 N
Therefore, upthrust acting on the object is 1.8 N.
Example 2
A body immersed in water displaces 1.1 N. If its weight while in water was 3.3 N, find its weight in air.

Solution
Weight of the displaced water = 1.1 N
Weight of the body in water = 3.3 N
upthrust = weight of an object in air − weight of an object in water
Upthrust = 1.1 N
Weight of the body in air = Apparent loss in weight + Apparent weight
= 3.3 N + 1.1 N = 4.4 N
Therefore, weight of the body in air is 4.4 N
Factors affecting upthrust
According to Archimedes’ principle, an object submerged in a fluid experiences
an upthrust that is equal to the weight of the fluid displaced. That is,
Upthrust (U) = Weight of displaced fluid (wf)
But,
Weight of the fluid displaced
(wf) = mass (mf) × acceleration due to gravity (g)
Mass of the fluid (mf) = density of the fluid(ρf ) × volume of the displaced fluid (Vf)
mf = ρfVf
In Chapter Four, you learned that the volume of the displaced fluid is equivalent to the volume of the immersed object.
That is,
Volume of the fluid displaced (Vf) = volume of object (V0) × acceleration due to gravity (g)
Since, Vf = Vo
mf = ρf/V0
U = mf g
Thus, U = ρfV0g
That is,
upthrust = density of the fluid × volume of the object × g
Hence, upthrust is affected by:
(i) the volume of the immersed object;
(ii) the density of the fluid in which the object is immersed; and
(iii) the acceleration due to gravity.
Example 3
Calculate the resulting buoyant force, if a steel ball of radius 6 cm is immersed in water. Assume density of water is 1 000 kg/m3 and acceleration due to gravity is 10 N/kg.


Example 4
A man whose weight is 690 N contains 5.3 × 10-3 m3 of blood. Calculate the weight of the blood if its density is 1 060 kg/m3.
Solution
Given data:
Volume of blood (V) = 5.3 × 10-3 m3
Density of blood (ρ) = 1060 kg/m3
Recall, w = mg, where m = ρV
w = (ρV)g = ρVg
= 1060 kg/m3 × 5.3 × 10-3 m3 × 10 N/kg
= 56.18 N
Exercise 1
1. (a) Explain the following terms in relation to the concept of sinking and floating.
(i) Buoyancy.
(ii) Apparent weight.
(iii) Actual weight.
(b) How is the apparent weight of an object in a fluid related to its actual weight in air?
2. An aluminium cube has a volume of 800 cm3. If it is totally immersed in water, calculate the upthrust acting on it. Assume density of water is 1 000 kg/m3 and acceleration due to gravity is 10 N/kg.
3. An iron piece of mass 360 g and a density of 7.8 g/cm3 is suspended by a rope so that it is partially submerged (halfway) in oil of density 0.9 g/cm3 . Find the tension in the string.
4. A body lost 0.6 N in weight when immersed in water. Calculate its volume in cubic centimetres.
5. State Archimedes’ principle and state its application in daily life.
6. Design an activity to verify Archimedes’ principle in the home environment.
7. Assume a body weighs X N in the air and experiences an upthrust of Y N in a liquid. Write the expression for apparent weight in terms of X and Y.
8. Why does a stone weigh more in air than when immersed in water?
Determination of relative density using the Archimedes’ principle
In Chapter Four, you learnt the concept of relative density (R.D) of a substance. The relative density of a substance was expressed as:


Activity 4
Aim: To determine the relative density of a stone using Archimedes’ principle.
Materials: Stone, spring balance, water, beaker and string
Procedure
1. Suspend the stone on a spring balance using the string, as shown in Figure 5.6 (a).
2. Record the reading on the spring balance.
3. Measure the weight of the stone in water while it is suspended on a string shown in Figure 5.6 (b).
4. Record your results.

Questions
(a) What is the weight of the stone in the air?
(b) What is the weight of the stone when immersed in water?
(c) Calculate the apparent loss in weight.
(d) Calculate the relative density of the stone.

Relative density of the stone can be calculated from the obtained results. For example, the stone weighs is 25 N in air and 17 N in water, then,

Activity 5
Aim: To determine the relative density of a solid that floats in water.
Materials: Cork, stone (sinker), spring balance, string, beaker and water
Procedure
1. Tie a stone with a string and suspend it from a spring balance. Record its weight as w1.
2. Immerse the stone in a beaker that contains water as shown in Figure (a).

3. Record its apparent weight as w2.
4. Using the same string, tie the cork so that it is above the stone.
5. Immerse the stone in water while the cork is in the air shown in Figure 5.7 (b).
6. Record their weight as w3.
7. Immerse both the stone and the cork in the water shown in Figure 5.7 (c) and
record their combined weight as w4.
Questions
(a) What is the function of a stone?
(b) From your results, fill in the following blanks.
|
(i) Weight of the stone in air, ( w1 ). |
____N |
|
(ii) Weight of the stone in water, ( w2 ). |
____N |
|
(iii) Weight of the stone in water + cork in air, ( w3 ). |
____N |
|
(iv) Combined weight of the stone + cork (both immersed), ( w4 ). |
____N |
|
(v) Weight of the cork in air is obtained by (w3 – w2). |
____N |
|
(vi) Apparent weight loss of the cork. |
____N |
(c) Calculate the relative density of the cork using the above information.

A sinker is a solid substance that sinks in water. In this case, it is used to sink with a body that floats on water. In Activity 5.5, the sinker is the stone and the cork is used as a floating body. Then, the relative density of the solid that floats can be calculated as follows,
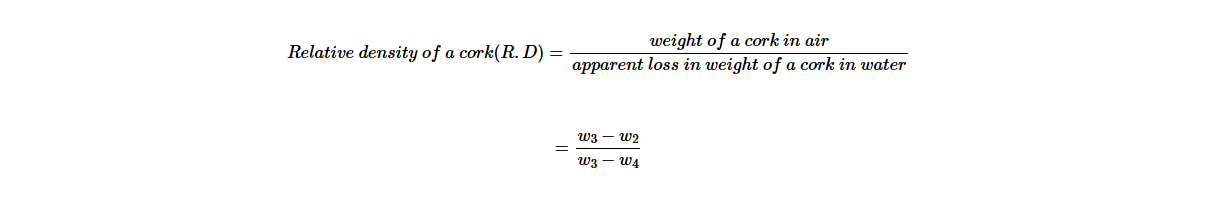
Task 5
Repeat Activity 5.5 using kerosene instead of water. How does the result compare to the one obtained in Activity 5.5? Give reasons for the observation.
Activity 6
Aim: To determine the relative density of kerosene, using Archimedes’ principle.
Materials: Stone, beaker, water and kerosene
Procedure
1.Using a spring balance, weigh the stone in the air. Record its weight in air as w1.
2. Weigh the stone when it is fully immersed in water inside a beaker and record its weight as w2.
3. Remove the stone from the water and dry it. Weigh the stone when fully immersed in kerosene and record its weight as w3.
Questions
(a) Calculate the upthrust in kerosene.
(b) Calculate the upthrust in water.
(c) Calculate the relative density of the kerosene.
(d) Compare the density of water and kerosene.

Upthrust in kerosene = weight of kerosene displaced
Upthrust in kerosene = w1 − w3
Upthrust in water = Weight of water displaced
= w1 − w2
Since an object immersed in a fluid displaces its volume of the fluid, and considering the relation for the relative density of a liquid,

Example 5
In an experiment to determine the relative density of a liquid, a solid Q weighed as follows:
Weight in air, w0 = 8.6 N
Weight in water, w1 = 6.0 N
Weight in liquid, w2 = 5.4 N.
Calculate the relative density of the liquid.
Solution
Upthrust in liquid = w0 − w2
= 8.6 N − 5.4 N = 3.2 N
Upthrust in water = w0 − w1
= 8.6 N − 6.0 N = 2.6 N
By Archimedes’ principle
Upthrust = weight of the displaced fluid
Note that, 1 g = 0.01 N,


Exercise 2
Whenever necessary use acceleration due to gravity g = 10 N/kg.
1. What volume of iron of density 7.8 g/cm3 must be attached to wood whose mass is 100 g and density of 0.5 g/cm3 if both iron and wood have to float under the water surface?
2. An object is hung from a spring balance. If it weighs 40 N in air and 30 N when immersed in water:
(a) Calculate the upthrust on the object.
(b) Determine the weight of the displaced water.
(c) What is the mass of the displaced water?
(d) What is the volume of the displaced water?
(e) Calculate the relative density of the object.
(f) Calculate the density of the object.
3. An object weighs 60 N when in air and 40 N when immersed in water. What is its:
(a) Relative density?
(b) Density?
4. A piece of sealing wax of helium weighs 0.27 N in air and 0.12 N when immersed in water. Deduce:
(a) its apparent weight in a liquid of density 800 kg/m3; and
(b) its relative density.
5. A metal cube of side 2 cm weigh 0.56 N in air. Determine:
(a) its apparent weights when immersed in the methylated spirit of density 0.585 g/cm3; and
(b) the density of the metal of which it is made.
Law of floatation
The previous sections have established that a body can float on a fluid if certain conditions are satisfied. This leads us to the law of floatation which states that:
‘A floating body displaces its own weight of the fluid in which it floats’. Activity 5.7 demonstrates the relationship between upthrust and floatation.
Activity 7
Aim: To investigate the relationship between upthrust and floatation..
Materials: Piece of wood, transparent beaker, water, spring balance, digital balance, weights
Procedure
1. Suspend a piece of wood from a hook of a spring balance shown in Figure 5.8 (a). Record its weight,
2. Weigh a dry and empty beaker shown in Figure (b).



3. Fill the transparent beaker with water to about 3/4 of its height and weight it as shown in Figure 5.8 (c).
4. Place the wood on the surface of the water and record its apparent weight.
5. Measure and record the water level when the wood is placed on the surface of the water.
6. Place a small weight on the floating wood.
7. Measure the water level and the depth of submersion of the wood after adding each weight.
8. Continue adding weights gradually, recording the water displacement and submersion depth each time, until the object begins to sink.
Question
(a) How the upthrust is related to the ability of the object to float?
(b) Describe the conditions under which the object floats or sinks, based on the balance between the weight of the object and the upthrust.

The upthrust of the floating piece of wood is zero. However as the weight of the object increases, the upthrust (or buoyant force) needs to increase for the object to remain floating, causing more of the object to become submerged. When the weight of the object exceeds the upthrust provided by the displaced water, the object will begin to sink.
Relationship between upthrust and floatation
Upthrust depends on the density of the fluid. If the density of an object is less than that of the surrounding fluid, the object will float. If the density of the object is larger than the density of the fluid, the object will sink.
This is the reason why an object seems lighter, for example, in salt water than in fresh water and appears to weigh less in water than in air. A ship floats more easily in the sea, and also it is easier to swim in the ocean than in the lake because sea water is denser than lake water. The Figure below shows a marine vessel floating in seawater.

For an object to float on a fluid the upthrust exerted on it by the fluid must be equal to the weight of the object. That is, U = w. Since, upthrust is equal to the weight of the displaced fluid, then,
Weight of the displaced liquid = Apparent loss in weight of the object.
But,
apparent loss in weight = upthrust.
And,
Upthrust = actual weight – apparent weight.
Since,
upthrust = weight of the object.
Then, for an object to float, its apparent weight must be zero.
Relationship between volume of submerged part of the floating body and the density of fluid
Consider, a cork in Figure 5.10 submerged in water of a particular volume and density. The two forces acting on a submerged body are upthrust U, and the weight of a floating body, wB. When an equilibrium is reached, these two forces balance. Hence,
The upthrust in a liquid = weight of the liquid displaced.

A cork submerged in water
Consider a body of volume V1 and density ρ1
Volume of submerged part is V2
Weight of the body, wB = V1ρ1g
Upthrust of the fluid U = V2ρ2g
From the principle of floatation;

Example 6
Suppose an 80 kg man floats in fresh water with 92% of his volume submerged when his lungs are full of air. What is his average density? Take the density of water to be 1 000 kg/m3.
Solution
Let the volume of a man = V1
Volume of the submerged body of a man = V2
Density of a man = ρperson
Density of water = ρwater
The man’s density can be obtained by solving the equation,

Example 7
Calculate the density of a wood, if a floating body is 98% submerged in water. Take the density of water to be 1000 kg/m3.

Solution
Given,
Density of water, ρ = 1 000 kg/m3
From Archimedes’ principle,
buoyant force = weight of the body
Fb = ρb ×Vb × g
Fb =Vbρbg
where, ρ, g, and V are the density of water, acceleration due to gravity, and volume of water and Vb and ρb are the volume and density of the body, respectively.
Since 98% of the body is immersed,
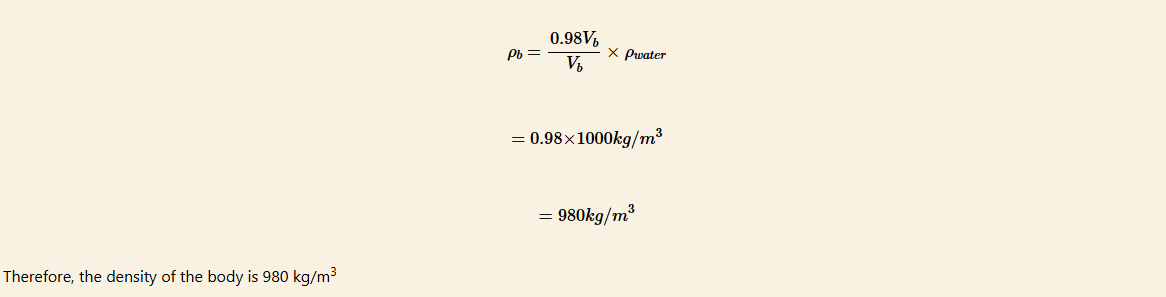
Law of floatation in everyday life
Some objects and vessels float or can be made to float. Balloons, canoes, ships,boats and submarines obey the law of flotation in their operations. These bodiesare designed in such a way that the average density of the body is less than the density of the fluid in which they float.
Therefore, an object made of a material of high density, such as a metal, must have a lot of space filled with material of very low density like air. Remember that an object will float if its average density is less than the density of the fluid in which it is immersed. The operation principles of various floating objects are discussed in the forthcoming sections.
Balloons
Suppose we have a 5.5 g balloon made of rubber, which has a density of 1.52 g/cm3.The volume of the balloon is 3.62 cm3. Since the density of rubber is much greaterthan the density of air (0.001293 g/cm3) a deflated balloon would not float in air. Now let us inflate the balloon with helium gas, which has a density of 0.000178 g/cm3. Suppose we put 3 000 cm3 of helium in the balloon.
The mass of this helium is 0.534 g, therefore the balloon has a total mass of 6.034 g and a total volume of 3 003.62 cm3.The density of the helium balloon becomes 0.00200 g/cm3, which is still greater than the density of air. Let us add 2500 cm3 more helium to the balloon. Now, the total mass is 6.479 g and the total volume is 5 503.62 cm3. The density of the helium balloon is now 0.00118 g/cm3, which is less than the density of air. The balloon will then float in the air.
Hot-air balloon
A hot-air balloon shown in Figure 5.11, consists of a bag called an envelope that is capable of containing hot air. Suspended beneath the envelope is the gondola, which carries a source of heat and passengers. As the temperature of the air in the envelope increases, it expands.
As the air expands, its volume increases while the mass remains constant resulting in a decrease in the density of air in the envelope. This makes the air in the envelope less dense than the cooler surrounding air. This difference in densities produces an upthrust that lifts the balloon and its passengers into the air.

A hot-air balloon can be made to rise or descend by changing the temperature of the air in the envelope. If the temperature is increased, the air expands more resulting to a greater upthrust causing the balloon to rise higher in air. If the air in the envelope is cooled, it contracts to a smaller volume producing less upthrust and thus lowering its height. You should note that the rise and fall of the hot-air balloon is influenced by factors such as the temperature of outside air and the variation of air density with altitude.
Example 8
A balloon made up of a fabric weighing 80 N has a volume of 1.0 × 107 cm3 . The balloon is filled with hydrogen of density 0.9 kgm-3. Calculate the greatest weight in addition to that of the hydrogen and the fabric, which the balloon can carry in air of an average density 1.25 kg/m-3.

Solution
Given,
Upthrust = weight of balloon and fabric + weight of hydrogen + greatest weight (i)
Upthrust = weight of the air displaced = volume of the air × density × gravity
(1.0 × 107 × 10−6 m3 × 1.25 kg/m-3 × 10 N/kg) = 10 × 1.25 × 10 = 125 N
Weight of hydrogen = Density of Hydrogen × volume × g
Weight of hydrogen = 0.90 kg/m3 × 1.0 × 107 × 10−6 m3 × 10 N/kg = 9 N
Therefore, by substituting these values in equation (i)
125 N = 80 N + 9 N + greatest weight
Hence, the greatest added weight = 125 N – 89 N = 36 N
Submarines
Submarines are made of steel and other dense materials with a lot of space filled with air because of the space the average density of the submarine is lower than that of seawater so it floats.
If we wish to submerge (sink) the submarine, seawater is allowed to flow into its ballast tanks until the average density of the submarine becomes greater than that of the seawater. To make the submarine resurface (float), air is forced into the ballast tanks pushing out the water until the submarine’s average density is again less than that of the seawater. Figure 5.12 shows a submarine floating on water.

Ships
A ship is made up of steel which is denser than water. One would expect the ship to sink in water due to the high density of steel. However, the ship has a large volume with a hollow space.
Large volume allows the ship to displace a large volume of water leading to a greater upthrust. Furthermore, the hollow space makes the average density of the ship to be less than the density of the seawater. Therefore, the ship floats on water.
When the ship is loaded, its mass increases, resulting to the increase of average density. This causes the ship to move lower into the water. Putting more load into the ship will make the ship to move deeper into the water.
If the load is increased beyond a certain limit, the ship will sink completely. Therefore, the amount of load in the ship must be controlled to avoid overloading. It is for this reason ships are marked with a special line which shows the maximum loading that the ship can take. This line is known as the Plimsoll lines, shown in Figure

Hydrometre
A hydrometre is an instrument used to determine the relative density of liquids. It is consists of a cylindrical stem which is graduated and a glass bulb at its end as shown in Figure.
The bulb is filled with mercury or lead ballast to make it float upright. The stem is made thin to allow a great change in height for a small change in density. The graduations in the stem of the hydrometre start with small numbers at the top and end with large numbers at the bottom, since, it sinks more in less dense liquids.

Structure of a hydrometre
A practical hydrometre has the following parts:
(a) a hollow narrow graduated glass tube or stem (T);
(b) a wide bulb (B); and
(c) a lead or mercury ballast to make the hydrometre float upright in liquid.
Note that the volume of the bulb determines the range of densities that can be measured. This is largely because the bulb sinks so as to push the surface of the liquid up to the stem. The narrower the stem, the more sensitive the hydrometer. This means that a small difference in density results to a large change of the reading on the stem.
Mode of action of hydrometre
A hydrometre is made to float in the liquid whose relative density is to be measured.It sinks to different levels depending on the relative density of the liquid in which it is floating, as shown in Figure.

The liquid whose relative density is to be determined is poured into a tall jar and the hydrometre is gently lowered into the liquid until it floats freely. The point where the surface of the liquid touches the stem of the hydrometre indicates the relative density of the liquid.
Remember that since the density of water is 1 g/cm3, the density of the liquid in g/cm3 is numerically equal to its relative density. Considering Figure 5.15, the hydrometre sinks more in methanol whose relative density is 0.8 and sinks less in water whose relative density is 1. This means that water is denser than methanol.
Determination of relative density of a liquid using hydrometer
Activity 8
Aim: To determine the relative density of a liquid.
Materials: Liquid, hydrometer, sand or lead ballast
Procedure
1. Take a thin-walled test tube of cross-section area A and put a strip of graduated graph paper inside it. Ensure that the strip is waterproofed.
2. Take a glass jar containing water.
3. Try to float the test tube in the vertical position and partially submerged in water. Let the density of water be ρ1.
4. Put some mass of sand or lead ballast in the test tube to make the bottom of the test tube slightly heavy and read the level of water on the graph paper. Record the reading as L1.
5. Replace water in the jar with the liquid whose density is ρ2 .
6. Again, record the level of the liquid on the graph paper as L2.
Since, the weight of the test tube with the mass is the same in both cases, the Upthrust of water on the test tube = upthrust of the liquid on the test tube.
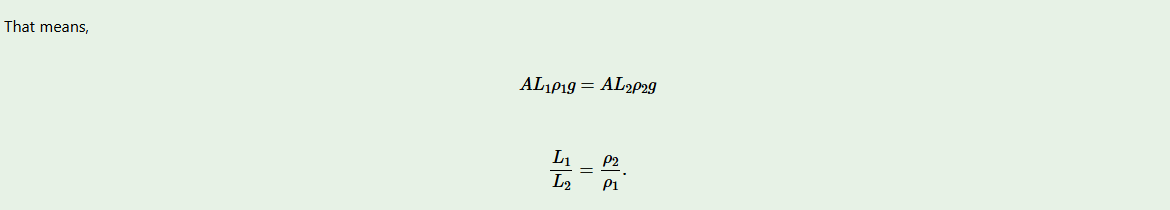

Example 9
The hydrometre shown in Figure 5.16 is used to measure the densities of liquids between 1 g/cm3 and 0.8 g/cm3. Assume that the density of water = 1 g/cm3, thecross-section area of the stem is 0.5 cm2 and the height of the stem above the liquid level is 16 cm. Determine the volume of the hydrometre below the 1.0 mark.

Solution
Let V1 cm3 be the volume of the hydrometre below 1.0 mark.
The volume between 0.8 and 1.0 marks be V2 cm3
The volume below the 0.8 mark be V3 cm3
Then, V2=Area×height =0.5cm2×16cm =8cm3
So, V3 = V1 + V2 = (V1 + 8) cm3
The upthrust on the hydrometre when in water is U = ρwater × V1 × g
Upthrust on the hydrometre when in the liquid U = ρliquid × V3 × g
From the law of floatation,
The weight of the hydrometre = upthrust in water = upthrust in liquid
That is
ρwater × V1 × g = ρliquid × V3 × g
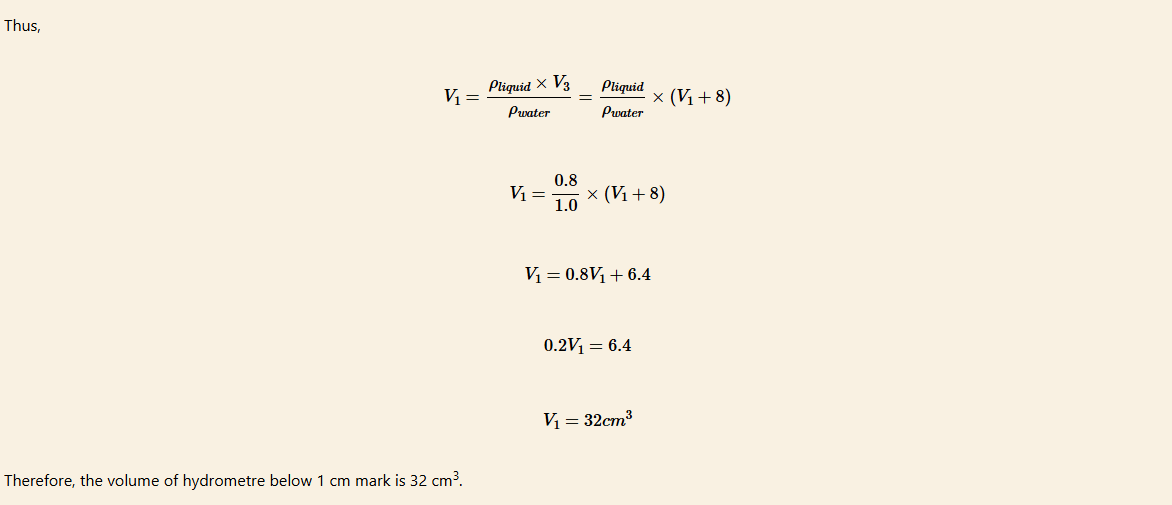
Chapter summary
1. An object immersed partially or totally in a fluid (liquid or gas) experiences an upward force called the buoyant force or upthrust.
2. The buoyant force causes the object to have an apparent weight that is less than its weight in the air. Apparent loss in weight = weight in air – weight in a fluid.
3. Archimedes’ principle states that ‘The upthrust on a body is equal to the weight of fluid displaced by the object. That is, upthrust = weight of displaced fluid.
4. The density and relative density of solid and liquid can be determined using Archimedes’ principle. The same principle applies whether determining density or relative density.

5. An object floats or sinks depending on its density and the density of the fluid in which it is placed.
6. An object will float if it displaces a weight of fluid equal to its own weight. In other words, an object will float if its density is less than the density of the fluid in which it is immersed.
7. Hot-air balloons, submarines, ships and weather balloons can be made to float by altering their volume to make them less dense than the fluid in which they float.
8. A hydrometre is a device used to measure the relative density of different liquids. It works on the principle that the hydrometre sinks until it displaces a volume of liquid that has the same weight as itself. The hydrometre sinks further in low density liquids than in high-density liquids.
Revision exercise
Section A
1. Choose the most correct answer.
(i) The same body is immersed in liquid A and then, in liquid B. The extent to which the body sinks in liquid B is less than in liquid A. What conclusion can be drawn from such an observation? The density of:
(a) the liquid A is more than that of liquid B.
(b) the liquid B is more than that of liquid A.
(c) the solid body is less than that of the liquid in both cases.
(d) the liquid A is the same as that of liquid B.
(ii) A sample of milk diluted with water has a density of 1040 kg/m3. If pure milk has a density of 1080 kg/m3, then, the percentage of water by volume in the diluted milk is:
(a) 55%.
(b) 40%.
(c) 50%.
(d) 45%.
(iii)A student lowers an object into a liquid filled in a container. He finds that there is a maximum apparent loss in weight of the object when:
(a) it just touches the surface of the liquid
(b) it is partially immersed and also touches the sides of the container.
(c) it is completely immersed in the liquid.
(d) it is partially immersed in the liquid.
(iv) The sea water is denser than freshwater due to:
(a) mixing of sand.
(b) stagnation.
(c) mixing salts.
(d) evaporation.
(v) Which of the following methods should be adopted in measuring the volume of the liquid displaced by a solid using a measuring cylinder?

(a) The solid should hang above the liquid surface in the jar, as in Figure 5.17 (III).
(b) The solid should be well inside the liquid, as in Figure 5.17 (I).
(c) Just rest at the surface of a liquid in the cylinder, as in Figure 5.17 (IV).
(d) The solid should be half immersed in liquid, as in Figure 5.17 (II)
(vi) A scuba diver wants to stay motionless at a specific depth in the water. What should the diver do to achieve this?
(a) Add weights to become more negatively buoyant.
(b) Inflate the buoyancy control device (BCD) to become more positively buoyant.
(c) Do not make any adjustments; the diver will automatically maintain neutral buoyancy.
(d) Kick their legs continuously to stay in place.
(vii) A student wants to compare the densities of two different liquids. Which instrument should the student use for a direct comparison?
(a) Barometer
(b) Thermometer
(c) Hygrometer
(d) Hydrometer
(viii) A ship sailing in the sea enters a wide and deep river. The density of seawater is 1 100 kg/m3, and the density of river water is 1 000 kg/m3.Determine a comparison of the volume of the object when it is in seawater to that when in river water.
(a) 11 : 10
(b) 10 : 11
(c) 121 : 100
(d) 1 : 1
(ix) If the relative density of a substance is 11.3, the density of the substance is,
(a) 11.3 kg/m3.
(b) 11.3 g/cm3.
(c) 11.3×10-3 g/m3.
(d) 11.3 × 103 g/cm3.
(x) How can a fish maintain its depth in water without continuously swimming?
(a) Fish have strong muscles that keep them suspended in water.
(b) Fish have specialized air sacks that help them control their buoyancy.
(c) Fish secrete oils that reduce their density and allow them to float.
(d) Fish use their fins to anchor themselves to the bottom of the water.
Section B
2. Explain the following scenario.
(a) You observe a stone and a leaf placed in a river. One sinks rapidly, and the other gently floats on the water’s surface. Explain the factors responsible for this difference in behaviour.
(b) You observe that an object submerged in water appears to weigh less than its actual weight. Describe the force responsible for this difference in weight.
(c) You have a book with a mass of 3 kg. Describe how the force of gravity determines the book’s actual weight on Earth.
3. When an object with a mass of 250 g is submerged in water, its weight is measured to be 2.2 N. What is the upthrust and the density of the object?
4. A ship has a mass of 1 000 tones and floats in seawater of density 1 023.6 kg/m3. Calculate the amount of water displaced.
5. When an object of mass 250 g and density 8 000 kg/m3 is submerged in methanol, which has a density of 0.79 g/cm3 , what would be its apparent weight? Use g = 10 m/s2
6. A 300 cm3 object weighs 2.5 N in air and 2 N in an unknown liquid. What is the density of the unknown liquid?
7. (a) A student places a hollow plastic ball and a solid plastic ball of the same size into water. The hollow ball floats, and the solid ball sinks. Explain the difference in their behaviour using Archimedes’ principle and the concept of density.
(b) Water ice has a density of 0.91 g/cm³, so it will float in liquid water. Imagine you have a cube of ice, 10 cm on a side.
(i) What is the cube’s weight?
(ii) What volume of liquid water must be displaced to support the floating cube?
(iii) How much of the cube is under the surface of the water?
8. Objects 1 and 2 are placed on opposite ends of a beam balance as shown in Figure 5.18. When held in air the two objects are seen to have the same weight. When lowered in water the objects are no longer balanced.


(a) Why the two objects which were initially balanced in air, appear imbalanced when immersed in water?
(b) Which object has the higher density? Explain your answer.
9. When an object of mass 200 g is submerged in the methanol, its apparent weight is 1.052 N. When submerged in benzene, its apparent weight is 0.951 N. If the density of methanol is 0.8 g/cm3, what is the density of benzene?
10. To measure the density of a 100 g block of wood, a 100 g lead sinker is attached to make the block sink as shown in Figure 5.19. When lowered into the water, the combination has an apparent weight of 1.3 N. If the density of lead is 11.3 g/cm3, what is the density of the wood?

11. A hot-air balloon including the envelope, gondola, burner fuel and one passenger has a total mass of 450 kg. The air outside the balloon is at 20 °C and has a density of 1.29 kg/m3. The air inside the envelope is heated to a temperature of 120 °C, at which it has a density of 0.90 kg/m3. What volume must the envelope expand in order to lift the balloon into the air?
12. A salvage ship is attempting to raise an iron anchor off the ocean floor. The anchor has a mass of 560 kg and the density of iron is 7 800 kg/m3. The cable used to lift the anchor can support a weight of 5 000 N before breaking. Use 1 025 kg/m3 as the density of seawater.
(a) Can the cable support the anchor while it is completely submerged?
(b) Can the cable support the anchor when it is completely out of the water?
(c) What percentage of the anchor will be out of the water when the cable breaks?
13. Icebergs are hazardous to shipping because so much of their volume is below the water level. If the density of seawater is 1 025 kg/m3 and the density of ice is 919 kg/m3 , what percentage of an iceberg is below the water level?